Question

In trapezium $ABCD$, $AB$ is parallel to $DC$; $P$ and $Q$ are the midpoints of $AD$ and $BC$ respectively. $BP$ produced meets $CD$ produced at point $E$. Prove that:
1. Point $P$ bisects $BE$,
2. $PQ$ is parallel to $AB$

Answer 1

Hint: The bisector is a line that separates a line or a point into two comparable parts. The bisector of a fragment consistently contains the midpoint of the portion.

Complete step-by-step solution:
Two lines are supposed to be parallel when they don't meet anytime on a plane. Lines that don't have a typical convergence point and never cross way with one another are parallel to one another. The symbol for indicating parallel lines is $\parallel $. The opposite distance between the two parallel lines is consistently steady. Consider squares, parallelograms, rectangles, and trapezoids; they all have parallel sides produced using parallel line sections.
By looking at the figure-

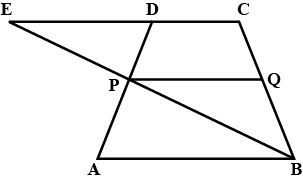
Given: $ABCD$ is a trapezium. $AB\parallel DC$. $P$ and $Q$ are midpoints of $AD$ and $BC$ respectively.
$BP$ produced meets $CD$ at $E$.
To prove: $P$ is the midpoint of $BE$.
1) In $\Delta PED$ and $\Delta ABP$
$\angle APB = \angle EPD$ (vertically opposite angles)
$\angle EDP = \angle PAB$ (alternate angles)
$PA = PD$ (P is the midpoint of AD)
Thus, $\Delta APB \cong \Delta DPE$ (ASA rule)
$PE = PB$ (by CPCT)
Thus, $P$ is the midpoint of $BE$.
Hence, P bisects BE.
2) For $\Delta ECB$,
$\eqalign{
  & PQ\parallel CE \cr
  & CE\parallel AB \cr} $
$PQ\parallel AB$
Hence proved.

Note: Two Triangles are said to be congruent when all corresponding sides and interior angles are congruent. The triangles will have a similar shape and size, but one may be a mirror image of the other. The symbol for congruent is $ \cong $. Two triangles are congruent when the three sides and the three angles of one triangle have the same measurements as three sides and three angles of another triangle.