Question

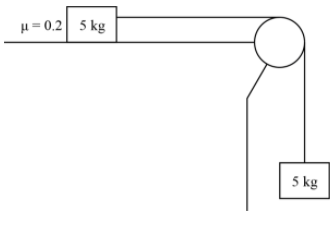
In this given figure, the magnitude of the acceleration of the centre of mass of the system is

Answer 1

Hint: This the pulley problem with two masses attached with one string over the pulley. First, you need to draw the Free Body Diagram of both the vertical and horizontal masses and then analyse it with Newton’s 2nd law of motion. Free body diagram shows us all the forces acting on the body apart from the whole system, hence the analysis gets easier.

Complete step by step answer:
The vertical and horizontal masses are the same, i.e., $m = 5\;{\rm{kg}}$
The table friction coefficient is $\mu = 0.2$

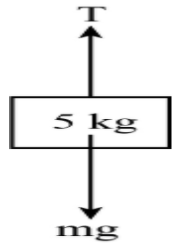
For vertical mass which is hanging outside the pulley, Newton’s 2nd law of motion applied to this mass. Then from Newton’s second law,
$mg - T = ma$
Putting the value of $m = 5\;{\rm{kg}}$ in the above equation,
$50 - T = 5a$ ……………………………. (1)
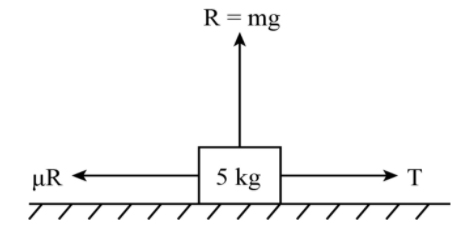
For Horizontal Mass.
From Newton’s second law
$T - \mu R = ma$
Putting the value of m,$\mu $ and $R$ in the above equation,
$T - 10 = 5a$ …………………………… (2)

The solution of equation (1) and (2) gives us the acceleration “a.”
Adding equation (1) and (2), we get
$\begin{array}{l}
10a = 40\\
\Rightarrow a = 4\;{\rm{m/se}}{{\rm{c}}^{\rm{2}}}
\end{array}$
The horizontal acceleration is calculated by
${a_x} = \dfrac{{{\rm{total}}\;\;{\rm{horizontal}}\;{\rm{force}}}}{{{\rm{total}}\;{\rm{mass}}}}$
So,
$\begin{array}{c}
{a_x} = \dfrac{{ma + 0}}{{m + m}}\\
\Rightarrow {a_x} = \dfrac{{50}}{{100}}\\
\Rightarrow {a_x} = 2\;{\rm{m/se}}{{\rm{c}}^{\rm{2}}}
\end{array}$
The vertical acceleration is calculated by
${a_y} = \dfrac{{{\rm{total}}\;{\rm{vertical}}\;{\rm{force}}}}{{{\rm{total}}\;{\rm{mass}}}}$
So,
$\begin{array}{c}
{a_y} = \dfrac{{0 + ma}}{{m + m}}\\
\Rightarrow {a_y} = \dfrac{{50}}{{100}}\\
\Rightarrow {a_y} = 2\;{\rm{m/se}}{{\rm{c}}^{\rm{2}}}
\end{array}$
Net acceleration can be calculated by using the expression,
\[a = \sqrt {{a_x}^2 + {a_y}^2} \]
Putting the value of ${a_x}$ and ${a_y}$
\[\begin{array}{l}
a = \sqrt {{2^2} + {2^2}} \\
\Rightarrow a = 2\sqrt 2 \;{\rm{m/se}}{{\rm{c}}^{\rm{2}}}
\end{array}\]
So, the net acceleration for the system is \[2\sqrt 2 \;{\rm{m/se}}{{\rm{c}}^{\rm{2}}}\].
Newton’s second law mostly governs pulley systems, and we can find out the tension in the string and acceleration by creating the equations for each mass in the system. There is another approach we can follow to solve these kinds of problems that use relative motion analysis. In a relative motion approach if both two objects have motion or acceleration, then we fix one object and continue the analysis of the 2nd object by implementing the effect of the first object on the 2nd.

So, the correct answer is “Option D”.

Note:
We used Newton’s 2nd law of motion for the analysis of two masses. You may go wrong in drawing the free body diagram with each and every force in the right direction. When the direction of the forces is not clearly mentioned in the free body diagram, then the equation may go unuseful.