Question

In this figure we see two non-uniform metre stick AB having the linear mass density variation$\lambda = {\lambda _0}x$, where ${\lambda _0}$is a constant and $x$is the distance from end A. It is placed on a smooth horizontal surface.

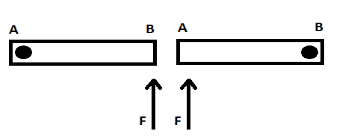
In the first experiment, the rod is pivoted at A and force F is applied perpendicular to the rod at the other end B and In the second experiment the rod is pivoted at B and the force applied is perpendicular to the rod at the end A. if in the first case angular acceleration is ${\alpha _A}$ and in the second case it is ${\alpha _B}$ then
A. ${\alpha _A} = {\alpha _B}$
B. ${\alpha _A} > {\alpha _B}$
C. ${\alpha _A} < {\alpha _B}$
D. Data insufficient to determine

Answer 1

Hint: the rotational inertia is calculated around a specific pivot point, which we choose A=0 for calculation and B=l. A non-uniform rod has mass density that varies from one end to another. In rod 1 we can see it is pivoted by the lighter end and rod b is pivoted by heavier end. This information will help us determine the relation between ${\alpha _A},{\alpha _B}$.

Complete step by step answer:
In rod 1 we can see in the figure it is pivoted at A and mass increases as we move towards B.

For rod 1
\[\lambda x = {\lambda _0}\left( {\dfrac{x}{L} + 1} \right)\]\[\]
${I_{rod1}} = \int\limits_{x = 0}^{x = L} {{\lambda _0}} (\dfrac{x}{L} = 1){x^2}dx$
$\Rightarrow{I_{rod1}} = {\lambda _0}{[\dfrac{1}{{4L}}{x^4} + \dfrac{1}{3}{x^3}]^L}_0$
$\Rightarrow {I_{rod1}} = \dfrac{7}{{12}}{\lambda _0}{L^3}$
Now for rod 2, we can see here it is pivoted by its heavier point that is B.

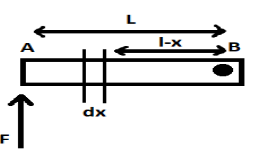
${I_{rod2}} = \int\limits_{x = L}^{x = 0} {dm{{(x - L)}^2}} $
$\Rightarrow{I_{rod2}} = \int\limits_{x = L}^{x = 0} {\lambda (x){{(x - L)}^2}( - dx)}$
Where we know \[\lambda x = {\lambda _0}\left( {\dfrac{x}{L} + 1} \right)\]
$
{I_{rod2}} = \int\limits_{x = 0}^{x = L} {{\lambda _0}} (\dfrac{x}{2} + 1){(x - L)^2}dx \\
\Rightarrow{I_{rod2}} = {\lambda _0}\int\limits_{x = 0}^{x = L} {(\dfrac{{{x^3}}}{L} - {x^2} - xL + {L^2})} dx \\
\Rightarrow{I_{rod2}} = \dfrac{5}{{12}}{\lambda _0}{L^3} \\
$
From this we get to know ${I_{rod2}} < {I_{rod1}}$.

On both the sticks the force applied is the same hence the torque produced will also be the same. Torque is denoted by $\tau = I\alpha $
We know that both the rod are similar and ${\tau _{rod1}} = {\tau _{rod2}}$
${I_{rod1}}{\alpha _A} = {I_{rod2}}{\alpha _B}$
By getting to know that ${I_{rod2}} < {I_{rod1}}$
We can automatically come to conclusion ${\alpha _A} < {\alpha _B}$

Hence, option C is the correct answer.

Note:If the same force is applied on two similar rods, note that magnitude of the torque will always be the same. In case of inequalities, when we have products of two quantities, the relationship remains the same. Thus, in the last step, the relationship between the Inertias will remain the same between $\alpha $.We take into consideration the axis of rotation and the pivot points because the mass density tends to increase when we move away from the origin.