Question

In this figure M is the midpoint of QR. \[\angle PRQ = {90^ \circ }\].

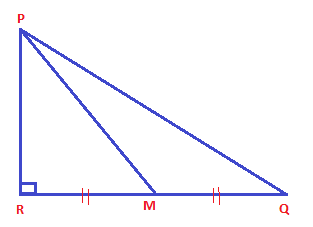
Prove that \[P{Q^2} = 4P{M^2} - 3P{R^2}\].

Answer 1

Hint:
Here in this geometrical problem we will take help of Pythagoras theorem. Because we are given that\[\angle PRQ = {90^ \circ }\]. So \[\vartriangle PRM = {90^ \circ }\] . Then we will modify the value of QR because we are given that M is the midpoint of QR.

Complete step by step solution:
Let’s consider \[\vartriangle PRM,\]
Applying Pythagoras theorem,
\[{(PM)^2} = {\left( {PR} \right)^2} + {\left( {RM} \right)^2} \to 1\]
Similarly for \[\vartriangle PRQ\]
\[{(PQ)^2} = {\left( {PR} \right)^2} + {\left( {RQ} \right)^2} \to 2\]
But it is given that m is the midpoint of QR. So above equation2 can be written as,
\[
   \Rightarrow {(PQ)^2} = {\left( {PR} \right)^2} + {\left( {RM + MQ} \right)^2} \\
   \Rightarrow {(PQ)^2} = {\left( {PR} \right)^2} + {\left( {2RM} \right)^2} \to \left( {\because RM = MQ} \right) \\
   \Rightarrow {(PQ)^2} = {\left( {PR} \right)^2} + 4{\left( {RM} \right)^2} \\
\]
Now from equation1
\[{\left( {RM} \right)^2} = {\left( {PM} \right)^2} - {\left( {PR} \right)^2}\]
Putting this value of \[{\left( {RM} \right)^2}\] in above equation we will get,
\[ \Rightarrow {(PQ)^2} = {\left( {PR} \right)^2} + 4\left[ {{{\left( {PM} \right)}^2} - {{\left( {PR} \right)}^2}} \right]\]
Multiplying the bracket with 4
\[
   \Rightarrow {(PQ)^2} = {\left( {PR} \right)^2} + 4{\left( {PM} \right)^2} - 4{\left( {PR} \right)^2} \\
   \Rightarrow {(PQ)^2} = + 4{\left( {PM} \right)^2} - 3{\left( {PR} \right)^2} \\
\]
Hence we proved the statement.

Note:
For this problem using Pythagoras theorem is the best approach to solve. Always focus on given data because it is the best indicator for leading a problem solution. The thought process is to think how we can get PQ in terms of PM and PR.