Question

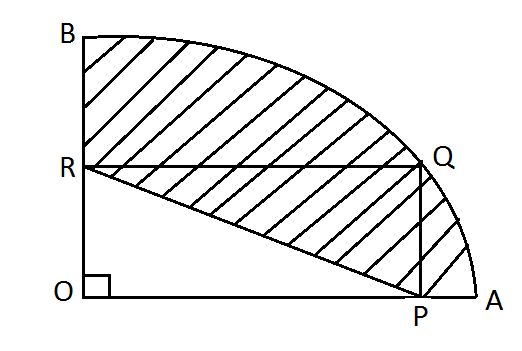
In this figure AOB is a quarter circle of radius 10 and PQRO is a rectangle of perimeter 26. The perimeter of the shaded region is

A. $13+5\pi $
B. $17+5\pi $
C. $7+10\pi $
D. $7+5\pi $

Answer 1

Hint: We will be using the concept of mensuration to solve the problem. We will use a formula for finding the perimeter of the circle to find the length of the quadrant and then we will find the length of the diagonal of the rectangle to find the required perimeter.

Complete step by step answer:
Now, we have to find the perimeter of shaded region given as

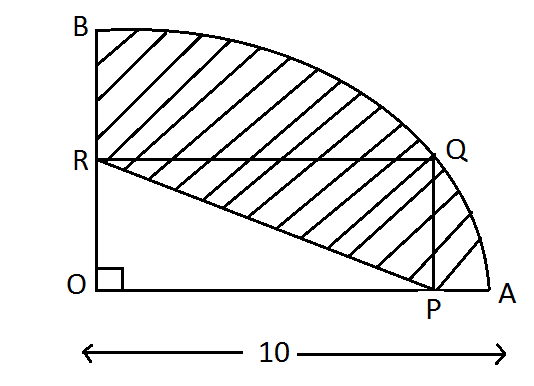
Now, we know that the length of arc $\overset\frown{BA}\ is\ \dfrac{1}{4}\left( 2\times \pi \times 10 \right)$
$=5\pi cm.............\left( 1 \right)$
Now, for the perimeter of the shaded region we have to find the sum of length of $BR+RP+PA+\overset\frown{AB}$.
Now, we know that the length of both diagonals of the rectangle is the same.
So, we have OQ = RP. Now, $OQ$ is the radius of the circle. Therefore,
$RP=10cm.........\left( 2 \right)$
Now, we have the perimeter of rectangle that is
\[RO+OP+PQ+RQ=26cm\]
We know that opposite sides of a rectangle are the same. Therefore,
$\begin{align}
  & 2\left( RO+OP \right)=26 \\
 & RO+OP=13cm \\
\end{align}$
Now, we can see from the figure that,
$\begin{align}
  & BR+PA=\left( BO-RO \right)+\left( OA-OP \right) \\
 & =BO+OA-\left( RO+OP \right) \\
\end{align}$
Now, BO = OA is the radius of a circle which is equal to 10cm.
Therefore,
$\begin{align}
  & BR+PA=20-\left( 13 \right) \\
 & =7cm \\
\end{align}$
Now, the perimeter of the shaded region is $BR+RP+PA+arc\overset\frown{BA}$.
Now, from (1), (2) and (3) we have,
$\begin{align}
  & =5\pi +10+7 \\
 & =\left( 17+5\pi \right)cm \\
\end{align}$

So, the correct answer is “Option B”.

Note: To solve these types of questions it is important to note the way we have found the length of individual parts and sum them up to find the perimeter of the shaded region also it is very important to note the way we have used the perimeter of the rectangle given to us to find the value of RO+OP.