Question

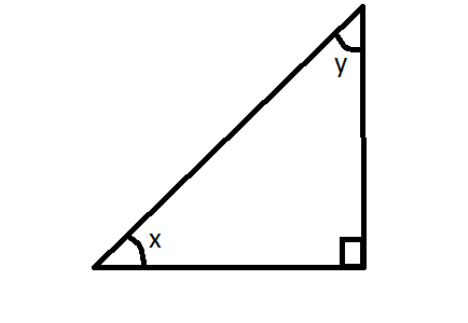
In the triangle above, the sine of $ x^\circ $ is 0.6. What is the cosine of $ y^\circ $ ?

Answer 1

Hint: We know, sine and cosine are the ratios of side to the hypotenuse of a right angled triangle. So, to solve this problem, we have to find the sine of $ x^\circ $ that resembles the ratio of which side to the hypotenuse of the triangle. Then we will find the cosine of $ y^\circ $ resembles the ratio of which side to the hypotenuse. Then by using the value for sine of $ x^\circ $ as given, we can find the required value, that is cosine of $ y^\circ $ .

Complete step by step solution:

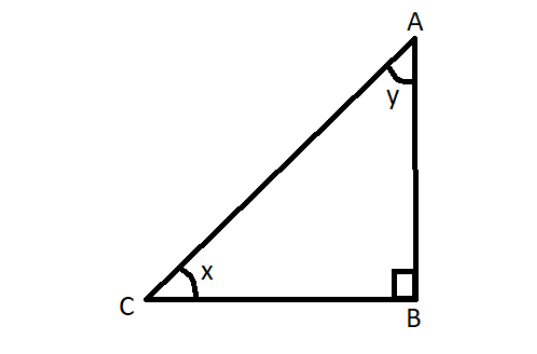
So, let us name the sides of the triangle as $ A,B,C $ , such that the right angle is at $ B $ .
The angle $ x^\circ $ is at $ C $ and the angle $ y^\circ $ is at $ A $ .
Now, we know, the sine of an angle is the ratio of the perpendicular to the hypotenuse in a right angled triangle.
Therefore, sine of $ x^\circ $ can be written as, $ \sin x = \dfrac{{AB}}{{AC}} = 0.6 $
Also, we know, cosine of an angle is the ratio of the base to the hypotenuse in a right angled triangle.
Therefore, we can write, cosine of $ y^\circ $ as, $ \cos y = \dfrac{{AB}}{{AC}} $
Therefore, it is clearly visible to us that, $ \sin x = \cos y = \dfrac{{AB}}{{AC}} $ .
So, we get a cosine of $ y^\circ $ as, $ \cos y = \dfrac{{AB}}{{AC}} = 0.6 $ .
So, the correct answer is “0.6”.

Note: We can also solve this problem in another way that is, if the sine of an angle is $ 0.6 = \dfrac{3}{5} $ , then the angle is $ 37^\circ $ , therefore, the other angle of the triangle other than right angle is clearly $ 53^\circ $ . Therefore, the cosine of $ 53^\circ $ is also $ 0.6 = \dfrac{3}{5} $ . The formulae of the trigonometric functions must be clearly understood before attempting such questions.