Question

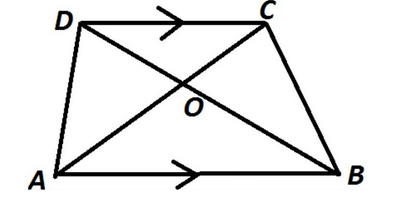
In the trapezium \[ABCD\] , \[AB\Updownarrow DC\] , \[AB\] \[=\] \[2CD\] and \[Ar(\vartriangle AOB)\] \[=\] \[84c{{m}^{2}}\] ,find the area of \[\vartriangle COD\] .

Answer 1

Hint: The arc of similar triangles are proportional to squares of their corresponding altitudes.
First we have to congruent the triangle by equaling the angles then area can be obtained by ratio method.
To congruent triangles use vertically opposite angle and alternative angle concept.

Formula used: \[\dfrac{Ar(\vartriangle AOB)}{Ar(\vartriangle COD)}=\dfrac{A{{B}^{2}}}{C{{D}^{2}}}\]
Area of two congruent triangle’s ratio is equal to the square ratio sides.


Complete step by step solution:
it is given that \[ABCD\] is trapezium and \[AB\Updownarrow DC\] .
In \[\vartriangle AOB\] and \[\vartriangle COD\] ,
 \[\angle ABO\] = \[\angle COD\]
 \[\angle BAO\] = \[\angle DCO\] Since: alternative angles are equal
 \[\angle AOB\] = \[\angle COD\] also, vertically opposite angles are equal
Therefore both the triangles are congruent
Hence,
 \[\begin{align}
  & \vartriangle AOB \\
 & \cong \\
 & \vartriangle DEF \\
\end{align}\]
We know that the arc of similar triangles are proportional to squares of their corresponding altitudes, therefore with \[Ar(\vartriangle AOB)\] \[=\] \[84c{{m}^{2}}\] and \[AB\] \[=\] \[2CD\] ,
We have,
Arc of \[\vartriangle AOB\] and arc of \[\vartriangle COD\] , taking their ratio and equating to the ratio of square of sides ,
 \[\dfrac{Ar(\vartriangle AOB)}{Ar(\vartriangle COD)}=\dfrac{A{{B}^{2}}}{C{{D}^{2}}}\]
Now: putting the value of the arc given, we can get :
 \[\Rightarrow \dfrac{84}{Ar(\vartriangle COD)}=\dfrac{4C{{D}^{2}}}{C{{D}^{2}}}\]
 \[\Rightarrow \dfrac{84}{Ar(\vartriangle COD)}=4\]
Getting the area of the given triangle,
 \[\Rightarrow Ar(\vartriangle COD)=\dfrac{84}{4}\]
 \[\Rightarrow Ar(\vartriangle COD)=21\;c{{m}^{2}}\]
Hence the given area is \[21\;c{{m}^{2}}\]
So, the correct answer is “\[21\;c{{m}^{2}}\] ”.

Note: \[AA\] similar triangle property is used here as angles are equal to both the alternative and vertically opposite angles of the trapezium .
Replace \[AB\] by \[CD\] by the given information in the ratio to get the equal on both the numerator and denominator to get the desired solution.
Area of triangles concept can be used in the ratio section.
Since \[AB\] parallel to \[CD\] and \[AC\] as transversal, alternative angles can be equal
We can also find the ratio of there areas as :
 \[4:1\]