Question

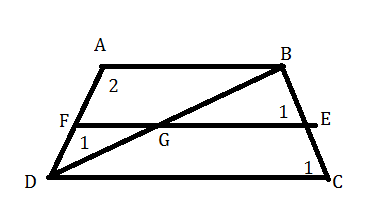
In the trapezium ABC, $\text{AB}\parallel \text{DA}$ and $\text{DC=2AB}$ .EF drawn parallel to AB cuts AD in F and BC in E such that $\dfrac{\text{BE}}{\text{EC}}=\dfrac{\text{3}}{4}$ . Diagonal DB intersects EF at G. Prove that, $7\text{FE=10AB}$ .

Answer 1

Hint: In the given question we can solve the question by proving triangle DFG and triangle DAB are similar to each other and in the similar triangles ratio of corresponding sides are equal.

Complete step by step answer:
In triangle DFG and triangle DAB
$\angle DFG=\angle DAB$ $\left\{ \begin{align}
  & \because FG||AB\, \\
 & \therefore \angle DFG=\angle DAB\,\text{due}\,\text{to}\,\text{corresponding}\,\text{angle} \\
\end{align} \right\}$
$\angle ADB=\angle FDG$ $\left\{ \because \,Common\,Angle \right\}$
$\therefore \angle DGF=\angle DBA$
So By AA similarity we can say \[\Delta DFG\approx \Delta DAB\]
So we can say the ratio of corresponding sides is equal.
$\dfrac{DF}{DA}=\dfrac{FG}{AB}$ .......................................................(i)
As in trapezium $EF||AB||DC$
 $\dfrac{AF}{DF}=\dfrac{BE}{EC}$
As given in question $\dfrac{BE}{EC}=\dfrac{3}{4}$
So we can write
$\dfrac{AF}{DF}=\dfrac{3}{4}$
On adding 1 in both side of equation
$\dfrac{AF}{DF}+1=\dfrac{3}{4}+1$
$\dfrac{AF+DF}{DF}=\dfrac{3+4}{4}$
$\dfrac{AD}{DF}=\dfrac{7}{4}$ $\left\{ \because AF+FD=AD \right\}$
$\dfrac{DF}{AD}=\dfrac{4}{7}$
We can use this value in equation (i)
Hence we have
$\dfrac{FG}{AB}=\dfrac{4}{7}$
$FG=\dfrac{4}{7}AB$......................................(ii)
Now in triangle compare $\Delta \text{BEG}$ and $\Delta \text{BCD}$ $\angle \text{BEG=}\angle \text{BCD}$ [corresponding angles ]
$\angle \text{B}=\angle \text{B}$ [ Common in both triangle ]
Now by AA criterion both and are similar.
$\therefore $$\Delta \text{BEG}$$\sim $ $\Delta \text{BCD}$ .
That will give us $\dfrac{\text{BE}}{\text{BC}}=\dfrac{\text{EG}}{\text{CD}}$ [similarity triangle]
Now we have given $\dfrac{\text{BE}}{\text{EC}}=\dfrac{\text{3}}{4}$
$\therefore $ $\dfrac{\text{EC}}{\text{BE}}$ $=\dfrac{4}{3}$
Add one both side $\dfrac{\text{EC}}{\text{BE}}+1=\dfrac{4}{3}+1$
  $\dfrac{\text{EC+BE}}{\text{BE}}=\dfrac{4+3}{3}$
 $\dfrac{\text{BC}}{\text{BE}}=\dfrac{7}{3}\text{ }\!\![\!\!\text{ BE+EC=BC }\!\!]\!\!\text{ }$
So, $\dfrac{\text{BE}}{\text{BC}}=\dfrac{3}{7}$
Got, $\dfrac{\text{BE}}{\text{BC}}=\dfrac{\text{EG}}{\text{CD}}$
 from above calculation
$\dfrac{\text{EG}}{\text{CD}}=\dfrac{3}{7}$
$\text{EG=}\dfrac{3}{7}\times \text{CD}$
We have,$\text{CD=2AB}$ (Given)
$\text{EG=}\dfrac{3}{7}\times \text{2AB}$ ...... (iii)
Now add (ii) and (iii) equations
$\text{FG+EG=}\dfrac{4}{7}\text{AB+}\dfrac{6}{7}\text{AB}$
$\Rightarrow \text{EF=}\dfrac{10}{7}\text{AB}$
$7\text{EF=10AB}$

Note: We can say two triangles are similar if all three sides or all three angles are equal. So if in two triangles two angles are equal then the third angle will also be equal. So from this rule we say triangles are similar to each other by AA similarity.