Question

In the transient shown the time constant of the circuit is

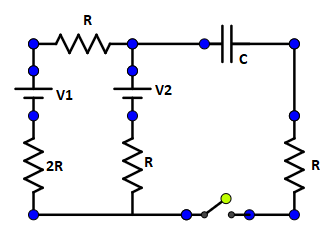
(A) $\dfrac{5}{3}\,RC$
(B) $\dfrac{5}{2}\,RC$
(C) $\dfrac{7}{4}\,RC$
(D) $\dfrac{7}{3}\,RC$

Answer 1

Hint:
In this question, the three resistance are connected in series and one resistance is connected in parallel. By using the resistance in series and resistance in the parallel formula, the total resistance is determined, then the time constant is determined.

Formula used:
The resistance in series is given by,
${R_s} = {R_1} + {R_2} + .......... + {R_n}$
Where, ${R_s}$ is the total resistance connected in series, ${R_1}$ is the resistance of the first resistor, ${R_2}$ is the resistance of the second resistor and ${R_n}$ is the resistance of the ${n^{th}}$ resistor.
The resistance in parallel is given by,
$\dfrac{1}{{{R_p}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ............. + \dfrac{1}{{{R_n}}}$
Where, ${R_p}$ is the total resistance connected in parallel, ${R_1}$ is the resistance of the first resistor, ${R_2}$ is the resistance of the second resistor and ${R_n}$ is the resistance of the ${n^{th}}$ resistor.

Complete step by step answer:
Now, the two resistances are connected in series, so by using the resistance connected in the series formula.
The resistance in series is given by,
${R_s} = {R_1} + {R_2} + .......... + {R_n}\,.............\left( 1 \right)$
By substituting the resistance value of the two resistors, then the above equation (1) is written as,
$\Rightarrow {R_s} = 2R + R$
By adding the resistance values, then the above equation is written as,
$\Rightarrow {R_s} = 3R$
Now, one resistance is connected parallel to the combined resistance ${R_s}$, then by using the resistance in parallel, then
$\dfrac{1}{{{R_p}}} = \dfrac{1}{{{R_s}}} + \dfrac{1}{R}$
By substituting the ${R_s}$ value in the above equation, then the above equation is written as,
$\Rightarrow \dfrac{1}{{{R_p}}} = \dfrac{1}{{3R}} + \dfrac{1}{R}$
By cross multiplying the above equation, then the above equation is written as,
$\Rightarrow\dfrac{1}{{{R_p}}} = \dfrac{4}{{3R}}$
Taking reciprocal, then the above equation is written as,
$\Rightarrow {R_p} = \dfrac{{3R}}{4}$
This equation shows the combined resistance of the three resistance.
Now, the one resistance is connected series to the combined resistance of the three resistance, then by using the resistance in series formula,
$\Rightarrow {R_s} = {R_p} + R$
By substituting the ${R_p}$ value in the above equation, then
$\Rightarrow {R_s} = \dfrac{{3R}}{4} + R$
By cross multiplying the above equation, then the above equation is written as,
$\Rightarrow {R_s} = \dfrac{{7R}}{4}$
From the above equation, the time constant $\tau $ is given as,
$\Rightarrow \tau = \dfrac{7}{4}RC$

$\therefore$ The required time constant is $\dfrac{7}{4}RC$. Hence, option (C) is the correct answer.

Note:
The resistance of the circuit is solved step by step only, if the resistance of the circuit is taken in a single equation, the solution may be wrong for some circuits. So, by solving this question more concentration is required while solving the resistances.