
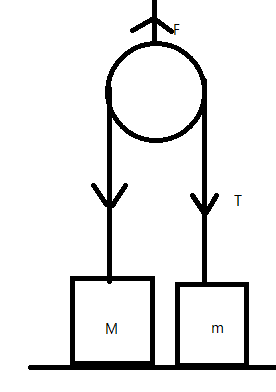
In the system shown, pulley and string are ideal. The vertical upward pull F is being increased gradually. Find the magnitude of F and acceleration of the $5\;kg$ block at the moment the $10\;kg$ leaves the floor.

Answer
579.3k+ views
Hint: We can assume the pulley-mass to be a system. There are two forces which act on the system. One is the tension on the string, and the other is the force due to gravitation. Then the resultant vector is the force acting on the whole system.
Formula used: $T=mg$
Complete step by step answer:
We know that a pulley is a simple device that can lift heavy objects with minimum energy. Here a block of some mass is attached to the pulley. A pulley consists of a tensile string or rope, which is used to tie and lift the heavy body and a shaft above which the string is kept. The shaft is circular generally and allows the easy movement of the string.
The force needed to lift the massive body is greater than the force needed to pull it using a pulley. Hence pulleys are used to lift heavy objects
Consider the pulley-mass system as shown in the figure. Where $M=10kg$ and $m=5kg$ is the mass of the blocks. Let $T$ be the tension on the string and $F$ be the force due to gravitation.
Clearly, we can say that $F=2T$
$\implies T=\dfrac{F}{2}$
We also know that $T=mg$
Just as the $10\;kg$ block leaves the floor, the tension experienced by the string is given as $T=10\times 10=100N$
Clearly, $F=2\times 100=200N$
At the same instant, let us assume that the block of mass $m=5kg$ is accelerated in the upward direction, say $a$.
Clearly, the total force on the block is given as $T-mg=F$
And also , $F=ma$
Then, we can say that $T-mg=ma$
Substituting the values we have, $100-50=5\times a$
$\implies a=10m/s^{2}$
Thus the net force $F$ acting in the upward direction is $200\;N$ and the acceleration of the body $m=5kg$ is $10m/s^{2}$
Note: Since tension and force are both vectors, the direction of the resultant force will be the addition of the two vectors using the parallelogram law of addition. Here only the force on the pulley is asked, hence the magnitude is sufficient.
Formula used: $T=mg$
Complete step by step answer:
We know that a pulley is a simple device that can lift heavy objects with minimum energy. Here a block of some mass is attached to the pulley. A pulley consists of a tensile string or rope, which is used to tie and lift the heavy body and a shaft above which the string is kept. The shaft is circular generally and allows the easy movement of the string.
The force needed to lift the massive body is greater than the force needed to pull it using a pulley. Hence pulleys are used to lift heavy objects
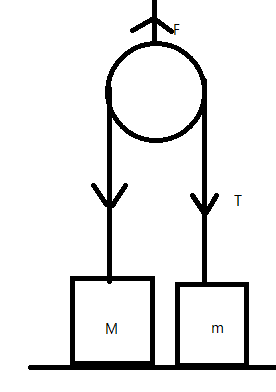
Consider the pulley-mass system as shown in the figure. Where $M=10kg$ and $m=5kg$ is the mass of the blocks. Let $T$ be the tension on the string and $F$ be the force due to gravitation.

Clearly, we can say that $F=2T$
$\implies T=\dfrac{F}{2}$
We also know that $T=mg$
Just as the $10\;kg$ block leaves the floor, the tension experienced by the string is given as $T=10\times 10=100N$
Clearly, $F=2\times 100=200N$
At the same instant, let us assume that the block of mass $m=5kg$ is accelerated in the upward direction, say $a$.
Clearly, the total force on the block is given as $T-mg=F$
And also , $F=ma$
Then, we can say that $T-mg=ma$
Substituting the values we have, $100-50=5\times a$
$\implies a=10m/s^{2}$
Thus the net force $F$ acting in the upward direction is $200\;N$ and the acceleration of the body $m=5kg$ is $10m/s^{2}$
Note: Since tension and force are both vectors, the direction of the resultant force will be the addition of the two vectors using the parallelogram law of addition. Here only the force on the pulley is asked, hence the magnitude is sufficient.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




