Question

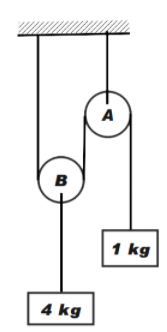
In the system shown in the given figure, the acceleration of 1 kg mass is.
                       

A. \[\dfrac{g}{4}\]downwards
B. \[\dfrac{g}{2}\]downwards
C. \[\dfrac{g}{2}\]upwards
D. \[\dfrac{g}{4}\] upwards

Answer 1

Hint: In this question we have been asked to calculate the acceleration of the block of mass 1 kg. We know that for a pulley system the mass and acceleration can be calculated using the equation of motion. Therefore, we shall first draw the free body diagram of the given system and write the equation based on the diagram and thus calculate the answer.

Complete answer:
In the given diagram, we can see that the 4 kg block is connected with an entirely different string. Therefore, we shall relate the tension between the strings.
Consider the FBD of pulley A, as shown in the diagram below.
             

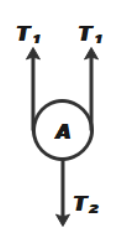
Now, from the above diagram we can say that,
\[2{{T}_{1}}-{{T}_{2}}={{m}_{a}}{{a}_{a}}\]
On solving,
\[2{{T}_{1}}={{T}_{2}}\]
Let us consider the free body diagram for block system as shown below,
         

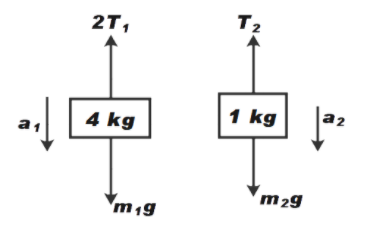
Now, to relate the strings we have constraint equation,
\[{{m}_{2}}=-{{T}_{2}}{{x}_{2}}\]
\[{{m}_{1}}=2{{T}_{1}}{{x}_{1}}\]
On solving,
We get,
\[2T{{x}_{1}}-T{{x}_{2}}=0\]
Therefore,
\[{{x}_{2}}=2{{x}_{1}}\]
Now, we know that differentiating twice the distance with respect to time we get acceleration
Therefore,
\[{{a}_{2}}=2{{a}_{1}}\] ……………. (1)
Now, from the free body diagram
We get,
\[{{m}_{2}}g-T={{m}_{2}}{{a}_{2}}\] ……………… (2)
Similarly,
\[2T-{{m}_{1}}g={{m}_{1}}{{a}_{1}}\] …………… (3)
After substituting the values in equation (2) and (3)
We get,
\[g-T=2{{a}_{1}}\] …………….. (since \[{{a}_{2}}=2{{a}_{1}}\])
\[2T-4g=4{{a}_{1}}\]
On solving above equations simultaneously
We get,
\[-2g=-8{{a}_{1}}\]
Therefore,
\[{{a}_{1}}=\dfrac{g}{4}\]……………….. (4)
Now from (1) and (4)
We get,
\[{{a}_{2}}=-\dfrac{g}{2}\]
The negative sign indicates that the acceleration of the block with 1 kg mass is upwards.

Therefore, the correct answer is option C.

Note:
The constraint equation is applied to find a relation between the motion of string i.e. the distance string moves due to acceleration on block. We know that work done by internal force is zero. If we consider the entire system as one unit, we get tension as the internal force. Therefore, using this concept the constraint equations are written.