Question

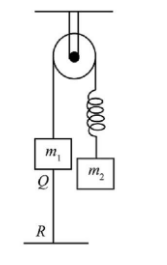
In the shown system ${m_1} > {m_2}$. Thread $QR$ is holding the system. If this thread is cut, then just after cutting:

(A) Acceleration of mass ${m_1}$ is zero and that of ${m_2}$ is direct upward
(B) Acceleration of mass ${m_2}$ is zero and that of ${m_1}$ is direct upward
(C) Acceleration of both the blocks will be same
(D) Acceleration of the system is given by $\dfrac{{\left( {{m_1} - {m_2}} \right)}}{{\left( {{m_1} + {m_2}} \right)}}\;kg$, where k is a spring factor

Answer 1

Hint: The given problem is based upon the application of Newton's motion. So here we will use the concept of a spring mass system. In the given problem figure, we can see that the mass of block ${m_1}$ is more than that of block ${m_2}$. As the thread QR is cut, then the resultant force on mass ${m_1}$ becomes equal to zero.

Complete step by step answer:
Given: Two blocks of different masses are given in the problem figure. The mass of one block attached to spring is ${m_2}$ and the mass of another block attached to thread QR is ${m_2}$.

In the given figure, the thread QR holds the system, then it says that the thread is cut, then just after cutting the resultant force on mass ${m_1}$ becomes equal to zero because we can see it is balanced by the tension in the spring. So the acceleration of the mass ${m_1}$ is zero.
${a_1} = 0$
Here, ${a_1}$ is the acceleration of mass ${m_1}$.

Now, we write the resultant force acting on mass ${m_2}$
${F_2} = \left( {{m_1} - {m_2}} \right)g$
Here, g is the acceleration due to gravity.

Now, we write the equation for acceleration acting in upward direction on mass ${m_2}$.
${a_2} = \dfrac{{{F_2}}}{{{m_2}}}$
Now, we substitute the value of ${F_2}$ in above relation.
${a_2} = \dfrac{{\left( {{m_1} - {m_2}} \right)g}}{{{m_2}}}$

Therefore, the acceleration of mass ${m_1}$ is zero and the acceleration of mass ${m_2}$ is directed upward and the correct option from the given options is option (A).

Note:In this type of problem we should know that the spring balances the system. If the thread is cut then, the mass at which the sting or thread is attached experiences zero resultant force and there is no change in the spring force.