Question

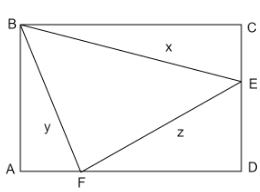
In the rectangle $ABCD$, what is the area of $\Delta BEF$ in terms of $x,y,z$ ?

Answer 1

Hint: First, we will find the length of all the sides and then compute the area of all triangles and the rectangle $ABCD$ , by solving all these equations and areas we will get the area of $\Delta BEF$ in terms of $x,y,z$ .

Complete answer:
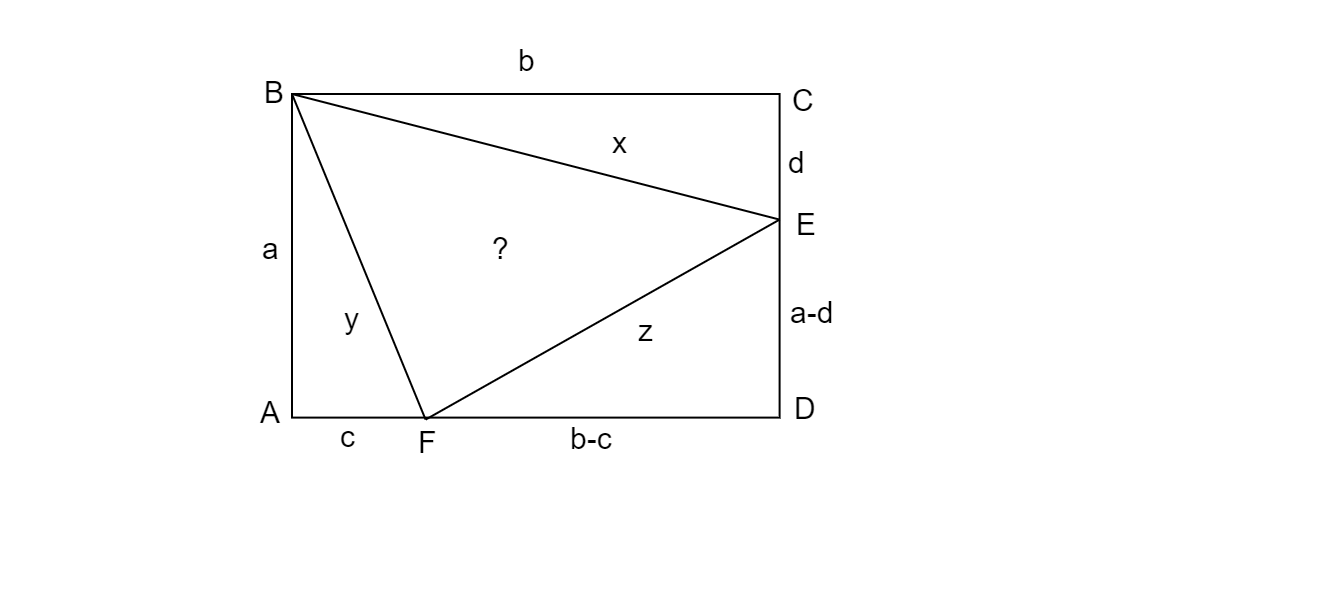
Let us assume the length of sides $AB = a,BC = b,AF = c,CE = d$ respectively.

Area of triangle = $\dfrac{1}{2} \times base \times height$
Consider $\Delta ABF$,
$\Rightarrow$ Area of $\Delta ABF$ = \[y\] …. (Given)
$\dfrac{1}{2} \times a \times c = y$
$c = \dfrac{{2y}}{a}$
Consider $\Delta BCE$,
Area of $\Delta BCE$ = $x$ …. (Given)
$\dfrac{1}{2} \times b \times d = x$
$d = \dfrac{{2x}}{b}$
$side{\text{ }}BC = side{\text{ }}AD = b$ …. (Opposite side of rectangle are congruent)
$side{\text{ }}AB = side{\text{ }}CD = a$ …. (Opposite side of rectangle are congruent)
$\Rightarrow$ $sideAD = sideAF + sideFD$ …. ($A - F - D$)
$b = c + sideFD$
$\therefore sideFD = b - c = b - \dfrac{{2y}}{a}$
$\Rightarrow$ $side\;CD = side\;CE + side\;ED$ …. ($C - E - D$)
$a = d + sideED$
$\therefore sideED = a - d = a - \dfrac{{2x}}{b}$
Consider $\Delta DEF$,
Area of $\Delta DEF$ = $z$ …. (Given)
$\Rightarrow$ $\dfrac{1}{2} \times \left( {b - \dfrac{{2y}}{a}} \right) \times \left( {a - \dfrac{{2x}}{b}} \right) = z$
$\Rightarrow$ $ab - 2x - 2y + \dfrac{{4xy}}{{ab}} = 2z$
$\Rightarrow$ $ab - 2x - 2y - 2z + \dfrac{{4xy}}{{ab}} = 0$
Multiplying both sides by $ab$ we get,
$\Rightarrow$ ${(ab)^2} - 2(ab)(x + y + z) + 4xy = 0$
This equation is a quadratic equation of form $a{x^2} + bx + c = 0$ and the roots of the equation are given by $x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$
Here, $x = ab,a = 1,b = - 2(x + y + z),c = 4xy$
$\therefore ab = \dfrac{{ - ( - 2(x + y + z)) \pm \sqrt {{{( - 2(x + y + z))}^2} - 4(1)(4xy)} }}{{2(1)}}$
$\therefore ab = \dfrac{{2(x + y + z) \pm \sqrt {4{{(x + y + z)}^2} - 16xy} }}{2}$
$\therefore ab = \dfrac{{2(x + y + z) \pm \sqrt {4[{{(x + y + z)}^2} - 4xy]} }}{2}$
Taking 4 common and inside the radical symbol and taking it out the radical sign we have,
$\therefore ab = \dfrac{{2(x + y + z) \pm 2\sqrt {{{(x + y + z)}^2} - 4xy} }}{2}$
Taking 2 common in the numerator, we have:
$\therefore ab = \dfrac{{2[(x + y + z) \pm \sqrt {{{(x + y + z)}^2} - 4xy} ]}}{2}$
cancelling 2, then we have,
$\therefore ab = (x + y + z) \pm \sqrt {{{(x + y + z)}^2} - 4xy} $
The area of rectangle $ABCD$ = $base \times height = a \times b = ab$
Substituting the value of $ab$ which we got by solving the quadratic equation, we get,
Area of rectangle $ABCD$ = $base \times height = a \times b = ab = (x + y + z) \pm \sqrt {{{(x + y + z)}^2} - 4xy} $
Consider the area of $\Delta BEF = \omega $,
Therefore, we can say
Area of rectangle $ABCD$ = area of $\Delta ABF$+ area of $\Delta BCE$ + area of $\Delta DEF$+ area of $\Delta BEF$
Substituting all the values we got into this equation we get,
$\Rightarrow$ $ab = x + y + z + \omega $
$\therefore (x + y + z) \pm \sqrt {{{(x + y + z)}^2} - 4xy} = (x + y + z) + w$
Since, $ab$ is the area of entire rectangle, it is larger than $(x + y + z)$ and hence we can reject the negative radical and consider only positive radical,
$\Rightarrow$ $w = \sqrt {{{(x + y + z)}^2} - 4xy} $
$\Rightarrow$ $\Delta BEF = \omega = \sqrt {{{(x + y + z)}^2} - 4xy} $
Therefore, the area of $\Delta BEF$ in terms of $x,y,z$ is $\sqrt {{{(x + y + z)}^2} - 4xy} $ .

Note:
Consider the sides of the rectangle and triangle as some constants and then form equations and find the solution of those equations. The area of a triangle inside a rectangle always has an area less than that of the rectangle.