Question

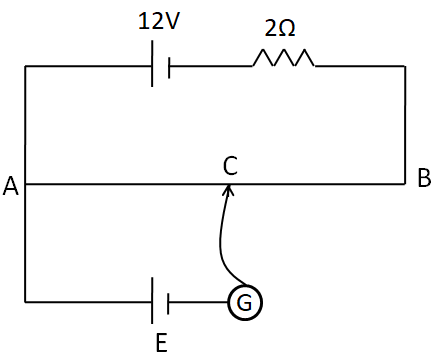
In the potentiometer circuit shown in the figure, the internal resistance of the $12{\text{V}}$ battery is $1\Omega $ and the length of the wire AB is $100cm$. When CB is $60cm$, the galvanometer shows no deflection. The emf of the cell ${\text{E}}$ is (the resistance of wire AB is $3\Omega $).

A. \[3.6{\text{V}}\]
B. ${\text{2}}{\text{.4V}}$
C. ${\text{3V}}$
D. $4.5{\text{V}}$

Answer 1

Hint: To solve this question, we need to balance the potential between the upper and the lower branch of the circuit across the wire AC. For this, we need to calculate the current in the circuit and the resistance of the wire AC.

Complete step-by-step solution:
According to the question, the length of the wire AB is $100cm$ and the length of CB is equal to $60cm$. So, the length of the wire AC becomes
$AC = AB - CB$
$ \Rightarrow AC = 100 - 60 = 40cm$
The resistance of the wire AB of length $100cm$ is given to be ${R_{AB}} = 3\Omega $.
So, the resistance of the wire AC becomes
${R_{AC}} = \dfrac{3}{{100}} \times 40$
$ \Rightarrow {R_{AC}} = 1.2\Omega $
Now, let $I$ be the current flowing in the circuit. The internal resistance of the battery is $r = 1\Omega $ and the external resistance connected in series has the value of $R = 2\Omega $. Also, the wire AB has the resistance of ${R_{AB}} = 3\Omega $. So the total resistance of the circuit becomes
${R_T} = R + r + {R_{AB}}$
$ \Rightarrow {R_T} = 2 + 1 + 3 = 6\Omega $
The value of the emf of the driver cell is equal to $12{\text{V}}$. So the current in the circuit becomes
$I = \dfrac{{12}}{6}$
$ \Rightarrow I = 2{\text{A}}$
So the potential difference between the points A and C becomes
${V_{AC}} = I{R_{AC}}$
\[ \Rightarrow {V_{AC}} = 2 \times 1.2 = 2.4{\text{V}}\]______(1)
From the lower branch containing the galvanometer, the potential difference between A and C is equal to the emf of the cell, that is,
${V_{AC}} = E$_________(2)
Equating (1) and (2) we get
$E = 2.4{\text{V}}$
Thus, the emf of the cell is equal to ${\text{2}}{\text{.4V}}$.
Hence, the correct answer is option B.

Note: The internal resistance of the test cell is not given in the question. This does not mean that it does not have it. It is not given in the question because it does not have any role in this question. This is because since there is no deflection in the galvanometer, no current will flow through the cell. So the internal resistance will not have any voltage drop across it.