Question

In the potentiometer circuit shown below, balancing length AJ when switch $S_1$ is closed and $S_2$ is open Is found to be 60 cm and that (AJ’) when $S_2$ is closed and $S_1$ is open is 80 cm. The unknown resistance x then is

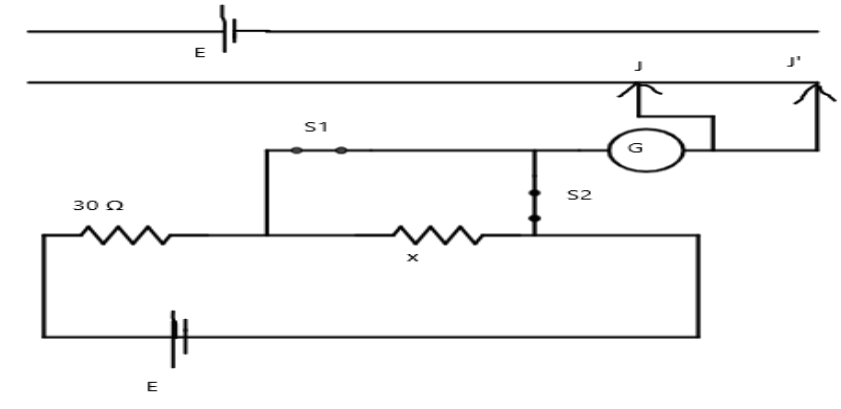
A) \[\;5\Omega \]
B) \[\;15\Omega \]
C) \[\;10\Omega \]
D) \[20\Omega \]

Answer 1

Hint: Consider a constant current that is flowing through a cross-section of area. It has the same composition and the potential drop across any length of the wire is directly proportional to the length. This is known as the principle of the potentiometer. The voltage developed in the circuit is directly proportional to the current and the resistance.

Formula used:
The emf of the cell or the potential drop of the cell, $\varepsilon = k{l_1}$ when \[{S_1}\]is closed and $k$ is the potential gradient ($\dfrac{v}{m}$).
The potential difference at the balance point,$V = k{l_2}$when ${S_2}$is closed and k is the potential gradient ($\dfrac{v}{m}$).
From Ohm’s Law, $V = IR$, where $R$ is the resistance.

Complete step by step solution:
Given details:
The position of the jockey in the first case, \[{l_1} = 80{\text{ }}cm\]
The position of the jockey in the second case,\[\;{l_2} = 60{\text{ }}cm\]
Given resistance, \[R = 30\Omega \]
Now we can use the above formulas to generate a relation between \[\;\varepsilon \] and $V$
Dividing the two equations, $\dfrac{\varepsilon }{V} = \dfrac{{{l_1}}}{{{l_2}}}$
Let $X$ be the unknown resistance of the cell. If the current I flow through cell when it is shunted with resistance $R$, then from Ohm’s Law we get $\varepsilon = I(R + x)$ and $V = IR$
Therefore, diving the equations we get,
$\dfrac{\varepsilon }{V} = \dfrac{{R + x}}{R}$=$\dfrac{{{{\text{l}}_1}}}{{{{\text{l}}_2}}}$
$ \Rightarrow \dfrac{{{\text{R + x}}}}{{\text{R}}} = \dfrac{{{{\text{l}}_1}}}{{{{\text{l}}_2}}}$
$ \Rightarrow 1 + \dfrac{{\text{x}}}{{\text{R}}} = \dfrac{{{{\text{l}}_1}}}{{{{\text{l}}_2}}}$
Taking the 1 to the right-hand side we get,
$ \Rightarrow \dfrac{{\text{x}}}{{\text{R}}} = \dfrac{{{{\text{l}}_1}}}{{{{\text{l}}_2}}} - 1$
$
   \Rightarrow {\text{x = R(}}\dfrac{{{{\text{l}}_1}}}{{{{\text{l}}_2}}} - 1) \\
    \\
 $
Now using the values, we get the value of$X$,
$ \Rightarrow {\text{x = 30(}}\dfrac{{80}}{{60}} - 1)$
$ \Rightarrow x = 30(\dfrac{8}{6} - 1)$
Dividing the terms, we get,
$ \Rightarrow x = 30(\dfrac{4}{3} - 1)$
$ \Rightarrow x = 30(\dfrac{1}{3})$
\[\therefore x = \;10\Omega \]

The correct option is (C).

Note:
Emf of a cell: The electromotive force of a cell is the maximum potential difference between two electrodes of a cell.
2. A potentiometer is used to measure the potential difference in a circuit.
3. Potentiometer is used to measure very small potential differences.
4. It shows a significant balancing length for a small change in the potential difference is measured.