Question

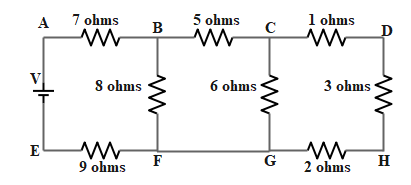
In the ladder network shown, current through the 3 ohms resistor is 0.25 A. The input voltage V is equal to
     

A. 1 V
B. 20 V
C. 5 V
D.5/2 V

Answer 1

Hint: In this question we have been asked to calculate the input voltage of the given circuit. We have been given a circuit diagram that consists of various resistors connected in series and parallel combinations. These resistors and battery form three different loops as shown in the figure. Therefore, to calculate the value of input voltage of the given circuit, we shall use Kirchhoff's loop rule for voltage or Kirchhoff’s voltage rule which states that in a loop of a circuit the sum of the voltage across the elements is zero.

Complete answer:
It is given that the current through the 3ohm resistor is 25 A.
Now, from the figure below,

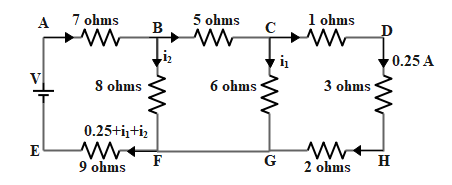
Applying the Kirchhoff’s loop rule to the loop CDGH, considering the direction of flow of current as positive
We get,
\[0.25\times 3+0.25\times 2-{{i}_{1}}\times 6=0\]
On solving,
\[1.5=6{{i}_{1}}\]
Therefore,
\[{{i}_{1}}=0.25\] ……………. (1)
Now, consider the loop BCGF
From Kirchhoff’s rule
We get,
\[5\left( 02.5+{{i}_{1}} \right)+6{{i}_{1}}-8{{i}_{2}}=0\]
Therefore,
\[{{i}_{2}}=0.5\] ………………… (2)
Now applying the Kirchhoff’s rule for the last loop with the battery
We get,
\[7\left( 0.25+{{i}_{1}}+{{i}_{2}} \right)+8{{i}_{2}}+9\left( 0.25+{{i}_{1}}+{{i}_{2}} \right)=V\]
After substituting the values from (1) and (2) in above equation
 We get,
\[V=7+4+9\]
Therefore,
\[V=20V\]

Therefore, the correct answer is option B.

Note:
The Kirchhoff’s law states that the algebraic sum of potential differences in any loop of a circuit must be equal to zero. While using the Kirchhoff’s the direction to go around the loop must be selected. It is very important to select a direction. If the value of the direction comes to be negative then the original direction of current flow is in the opposite direction.