Question

In the HCl molecule, the separation between the nuclei of two atoms is about \[1.27\,\mathop {\text{A}}\limits^{\text{o}} \](\[1\,\mathop {\text{A}}\limits^{\text{o}} = {10^{ - 10}}\,{\text{m}}\]). The approximate location of the center of mass of the molecule, assuming the chlorine atom to be about 35.5 times massive as hydrogen is
A. \[1\,\mathop {\text{A}}\limits^{\text{o}} \]
B. \[1.5\,\mathop {\text{A}}\limits^{\text{o}} \]
C. \[1.24\,\mathop {\text{A}}\limits^{\text{o}} \]
D. \[2.5\,\mathop {\text{A}}\limits^{\text{o}} \]

Answer 1

Hint: Use the formula for the position of the center of mass of two objects. Assume that the center of mass is at the origin and hydrogen and chlorine atoms are on either sides of the origin.

Formula used:
The position \[{x_{CM}}\] of the center of mass of two objects from the origin is
\[{x_{CM}} = \dfrac{{{m_1}{x_1} + {m_2}{x_2}}}{{{m_1} + {m_2}}}\] …… (1)
Here, \[{m_1}\] and \[{m_2}\] are the masses of two objects and \[{x_1}\] and \[{x_2}\]are the positions of the two objects of masses \[{m_1}\] and \[{m_2}\]from the origin respectively.

Complete step by step answer:
In the HCl molecule, the separation between the nuclei of two atoms is about \[1.27\,\mathop {\text{A}}\limits^{\text{o}} \].
Let \[{m_H}\] be the mass of the hydrogen atom and \[{m_{Cl}}\] be the mass of the chlorine atom.
The mass of the chlorine atom is 35.5 times more than the hydrogen atom.
\[{m_{Cl}} = 35.5{m_H}\]
The diagram representing the position of center of mass of HCl molecule is as follows:

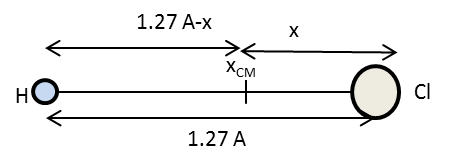
In the above diagram, \[x\] is the distance of chlorine atom from the origin and \[1.27\,\mathop {\text{A}}\limits^{\text{o}} - x\] is the distance of hydrogen atom from the origin.
Let the center of mass of HCl molecules is at the origin.
Determine the position of the center of mass of HCl molecules.
Substitute \[0\] for \[{x_{CM}}\], \[{m_{Cl}}\] for \[{m_1}\], \[{m_H}\] for \[{m_2}\], \[x\] for \[{x_1}\] and \[ - \left( {1.27\,\mathop {\text{A}}\limits^{\text{o}} - x} \right)\] for \[{x_2}\] in equation (1).
\[0 = \dfrac{{{m_{Cl}}x + \left[ {{m_H} - \left( {1.27\,\mathop {\text{A}}\limits^{\text{o}} - x} \right)} \right]}}{{{m_{Cl}} + {m_H}}}\]
\[0 = \dfrac{{{m_{Cl}}x - {m_H}\left( {1.27\,\mathop {\text{A}}\limits^{\text{o}} - x} \right)}}{{{m_{Cl}} + {m_H}}}\]
Substitute \[35.5{m_H}\] for \[{m_{Cl}}\] in the above equation.
\[0 = \dfrac{{35.5{m_H}x - {m_H}\left( {1.27\,\mathop {\text{A}}\limits^{\text{o}} - x} \right)}}{{35.5{m_H} + {m_H}}}\]
\[ \Rightarrow 35.5{m_H}x - {m_H}1.27\,\mathop {\text{A}}\limits^{\text{o}} + {m_H}x = 0\]
\[ \Rightarrow 35.5x - 1.27\,\mathop {\text{A}}\limits^{\text{o}} + x = 0\]
\[ \Rightarrow 36.5x - 1.27\,\mathop {\text{A}}\limits^{\text{o}} = 0\]
\[ \Rightarrow x = \dfrac{{1.27\,\mathop {\text{A}}\limits^{\text{o}} }}{{36.5}}\]
\[ \Rightarrow x = 0.0347\,\mathop {\text{A}}\limits^{\text{o}} \]
\[ \Rightarrow x \approx 0.035\,\mathop {\text{A}}\limits^{\text{o}} \]
Hence, the location of the center of mass of HCl molecules is \[0.035\,\mathop {\text{A}}\limits^{\text{o}} \] from the chlorine atom.
The position of the center of mass from hydrogen atom is
\[1.27\,\mathop {\text{A}}\limits^{\text{o}} - 0.035\,\mathop {\text{A}}\limits^{\text{o}} = 1.235\,\mathop {\text{A}}\limits^{\text{o}} \]

Therefore, the approximate position of the center of mass from the hydrogen atom is \[1.24\,\mathop {\text{A}}\limits^{\text{o}} \].

So, the correct answer is “Option C”.

Note:
The distance of hydrogen atom from the center of mass is taken negative as the hydrogen atom is on the left side of the origin (center of mass).
The center of mass is at the origin and hydrogen and chlorine atoms are on either sides of the origin.