
In the given parallelogram PQRS in which OX || SY. Prove that QX = SY.

Answer
584.1k+ views
Hint: To prove that OX = SY, we will use the rules of congruency. We know that the length of corresponding sides of congruent triangles are equal. Thus, we will prove that triangle QXP is congruent to triangle SYR. Congruence can be proved by two methods, viz. SAS test and ASA test. For the SAS test, we need to show that two sides and angles between them are the same and for the ASA test, we have to show that two angles and angles between them are the same. Once we prove that the two triangles are congruent, we can prove that QX = SY.
Complete step by step answer:
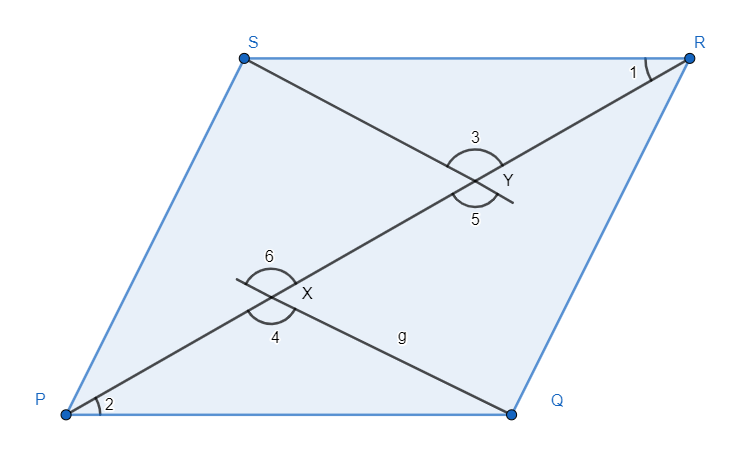
It is given to us that PQRS is a parallelogram.
The following figure is given to us.
We know that opposite sides of a parallelogram are equal and parallel to each other. This means PQ = SR and RQ = SP.
As we can see, PR is the diagonal of the parallelogram PQRS.
The diagonal acts as the transverse to parallel sides PQ and RS.
Therefore, angle RPQ is equal to angle PRS, that is ∠1 = ∠2……(1)
The diagonal is transversal to segments XQ and YS.
So, ∠4 = ∠5, as they are corresponding angles of parallel lines.
Now, we can also see that ∠3 = ∠5, as they are vertically opposite angles.
So, we can safely say that ∠4 = ∠3……(2)
We know that the sum of the angles of a triangle is 180°.
Therefore, in triangle SYR, ∠3 + ∠1 + ∠SYR = 180°
Thus, ∠SYR = 180° ─ (∠3 + ∠1).
Again, in triangle QXP, ∠4 + ∠2 + ∠QXP = 180°
Thus, ∠QXP = 180° ─ (∠4 + ∠2).
But we already showed that ∠4 = ∠3 and ∠1 = ∠2.
Therefore, ∠QXP = 180° ─ (∠3 + ∠1) = ∠SYR……(3)
Hence, in triangle SYR and triangle QXP,
PQ = SR……(opposite sides of parallelogram)
∠1 = ∠2……from (1)
∠QXP = ∠SYR……from (3)
Thus, by ASA rule, triangle SYR and triangle QXP are congruent.
We know that the length of the sides of two congruent triangles are equal.
Therefore, QX = SY.
Hence proved.
Note: The question can be solved with the basic knowledge of parallel lines and triangles. Students are advised to observe and study the figure very carefully as most of the information is only given in graphical form and not in textual form.
Complete step by step answer:
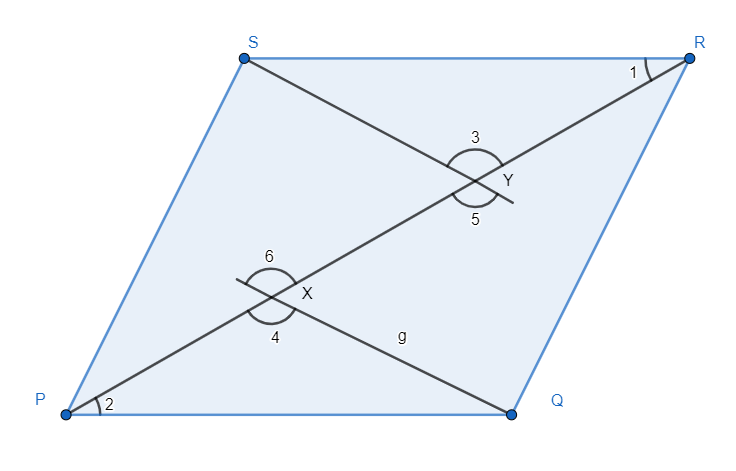
It is given to us that PQRS is a parallelogram.
The following figure is given to us.

We know that opposite sides of a parallelogram are equal and parallel to each other. This means PQ = SR and RQ = SP.
As we can see, PR is the diagonal of the parallelogram PQRS.
The diagonal acts as the transverse to parallel sides PQ and RS.
Therefore, angle RPQ is equal to angle PRS, that is ∠1 = ∠2……(1)
The diagonal is transversal to segments XQ and YS.
So, ∠4 = ∠5, as they are corresponding angles of parallel lines.
Now, we can also see that ∠3 = ∠5, as they are vertically opposite angles.
So, we can safely say that ∠4 = ∠3……(2)
We know that the sum of the angles of a triangle is 180°.
Therefore, in triangle SYR, ∠3 + ∠1 + ∠SYR = 180°
Thus, ∠SYR = 180° ─ (∠3 + ∠1).
Again, in triangle QXP, ∠4 + ∠2 + ∠QXP = 180°
Thus, ∠QXP = 180° ─ (∠4 + ∠2).
But we already showed that ∠4 = ∠3 and ∠1 = ∠2.
Therefore, ∠QXP = 180° ─ (∠3 + ∠1) = ∠SYR……(3)
Hence, in triangle SYR and triangle QXP,
PQ = SR……(opposite sides of parallelogram)
∠1 = ∠2……from (1)
∠QXP = ∠SYR……from (3)
Thus, by ASA rule, triangle SYR and triangle QXP are congruent.
We know that the length of the sides of two congruent triangles are equal.
Therefore, QX = SY.
Hence proved.
Note: The question can be solved with the basic knowledge of parallel lines and triangles. Students are advised to observe and study the figure very carefully as most of the information is only given in graphical form and not in textual form.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




