Question

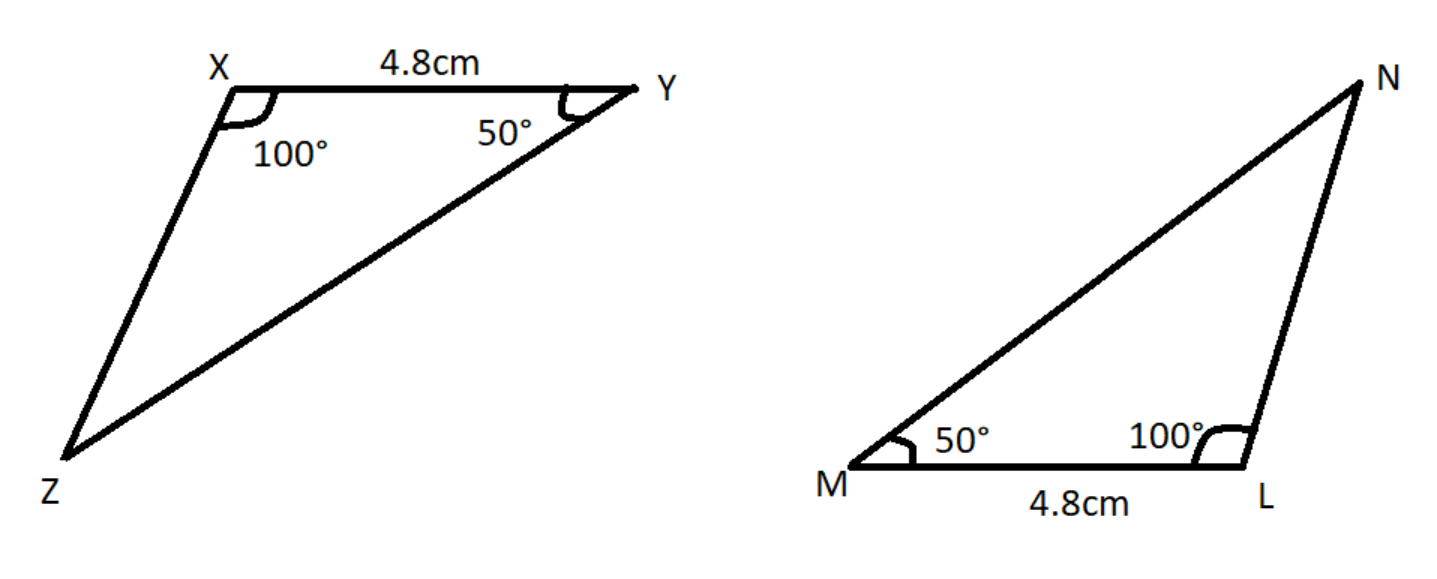
In the given pair of triangles, applying only the ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.

Answer 1

Hint: To solve this question, we need to have a strong idea about the different congruence rules and criteria. There are totally 5 congruence criteria.
SSS (side-side-side)
SAS (side-angle-side)
ASA (angle-side-angle)
AAS (angle-angle-side)
RHS (right angle-hypotenuse-side)
In this question, we are asked to use only ASA congruence criterion. The definition of ASA congruence criterion is:
The two triangles are said to be congruent to each other by this rule, if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle. When we proved that two triangles are congruent by this rule, the other angle and two sides will also be equal.
Using this rule, we will try to prove the congruence of the two triangles.

Complete answer:
Let’s first write down the given information:
There are two triangles:
In $\vartriangle XYZ$ :
$\angle ZXY = 100^\circ $
$\angle XYZ = 50^\circ $
$XY = 4.8$
In $\vartriangle LMN$ :
$\angle NLM = 100^\circ $
$\angle LMN = 50^\circ $
$ML = 4.8$
Now after writing down the given data, let’s define the ASA congruence criterion.
ASA Congruence Criterion: The two triangles are said to be congruent to each other by this rule, if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle. When we proved that two triangles are congruent by this rule, the other angle and two sides will also be equal.
Let’s write down the corresponding equal parts in both the triangles:
$\angle ZXY = \angle NLM = 100^\circ $ (A)
$XY = ML = 4.8$ (S)
$\angle XYZ = \angle LMN = 50^\circ $ (A)
Therefore, we can say that: $\vartriangle XYZ \cong \vartriangle LMN$ by ASA rule.
The above representation is a symbolic form of writing that two triangles that are congruent.

Note:
Students make a common mistake of assuming ASA congruence criterion and AAS congruence criterion are the same. They are slightly different from each other. In ASA, the side that is equal should be the included side. But in AAS, the side that is equal need not be the included side.
We also have to be careful while writing the symbolic form.
The symbol: $ \cong $ means that the two triangles are congruent.
The symbol: $ \sim $ means that the two triangles are similar.
Knowing the definitions of different congruence criteria will be beneficial in solving problems like this.