Question

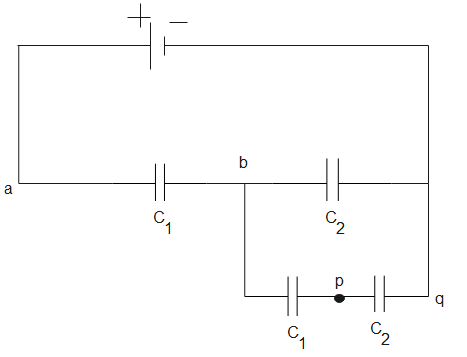
In the given network the potential difference between p and q is 2V and $C_2 = 3C_1$ . Then find the potential difference between a and b in V .

Answer 1

Hint: The figure shows capacitors connected in different combinations between different points. The capacitance is the product of charge and potential of the capacitor. Using this relation and solving the combination of capacitors, we can calculate the potential difference between the given points.
Formulas used:
$C=\dfrac{Q}{V}$

Complete answer:
Given, the potential difference between p and q is $2V$

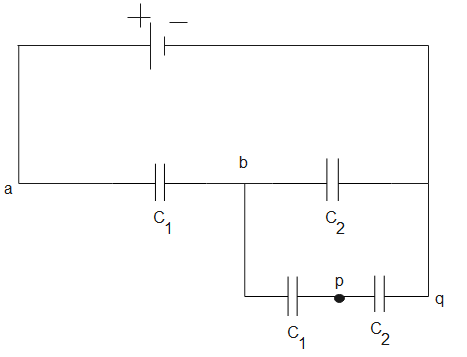
From the figure, we can say that the potential difference between p and q is equal to the potential difference across the capacitor ${{C}_{2}}$
We know that,
$C=\dfrac{Q}{V}$ - (1)
Here, $C$ is the capacitance
$Q$ is the charge on the capacitor
$V$ is the potential difference across the capacitor
For capacitor ${{C}_{2}}$, ${{V}_{2}}=2V$ substituting given values in the above equation, we get,
$\begin{align}
  & {{C}_{2}}=\dfrac{{{Q}_{1}}}{2V} \\
 & \Rightarrow {{Q}_{1}}=2{{C}_{2}}V \\
\end{align}$
Therefore, the charge on the capacitor ${{C}_{2}}$ is $2{{C}_{2}}V$.
The capacitors between the points b and q are in series, they will be related as-
$\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{{{C}_{2}}}{{{C}_{1}}}$
Given, ${{C}_{2}}=3{{C}_{1}}$, ${{V}_{2}}=2V$. In the above equation, substituting given values to get,
$\begin{align}
  & \dfrac{{{V}_{1}}}{2V}=\dfrac{3{{C}_{1}}}{{{C}_{1}}} \\
 & \Rightarrow {{V}_{1}}=6V \\
\end{align}$
Therefore, the potential drop across the capacitor ${{C}_{1}}$ is $6V$.
The total potential across bq is-
${{V}_{1}}+{{V}_{2}}=6V+2V=8V$ - (2)
The capacitors between b and q are connected in series, so the equivalent capacitance between b and q is-
$\begin{align}
  & \dfrac{1}{C}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}} \\
 & \Rightarrow \dfrac{1}{C}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{3{{C}_{1}}} \\
 & \Rightarrow \dfrac{1}{C}=\dfrac{4}{3{{C}_{1}}} \\
 & \therefore C=\dfrac{3{{C}_{1}}}{4} \\
\end{align}$
Now capacitors $\dfrac{3{{C}_{1}}}{4}$ and ${{C}_{2}}$ are in parallel.

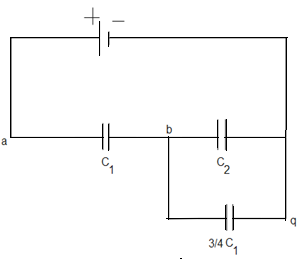
The equivalent capacitance between b and q is-
$\begin{align}
  & C'=\dfrac{3{{C}_{1}}}{4}+{{C}_{2}} \\
 & \Rightarrow C'=\dfrac{3{{C}_{1}}}{4}+3{{C}_{1}} \\
 & \Rightarrow C'=\dfrac{15{{C}_{1}}}{4} \\
\end{align}$
The total charge across bq will be-
$\begin{align}
  & Q=\dfrac{15{{C}_{1}}}{4}(8V) \\
 & \Rightarrow Q=30{{C}_{1}}V \\
\end{align}$

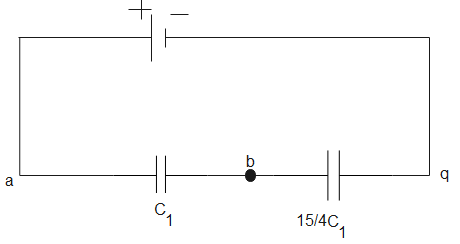
The charge across ${{C}_{1}}$ and $\dfrac{15{{C}_{1}}}{4}$ is the same as they are connected in series and the charge is $30{{C}_{1}}V$ (from eq (2)).
Using eq (1), the potential difference between a and b is-
$\begin{align}
  & V=\dfrac{30{{C}_{1}}V}{{{C}_{1}}} \\
 & \Rightarrow V=30V \\
\end{align}$
Therefore, points ab have a potential difference of $30V$.

Note:
Capacitors connected in series have the same charge while the capacitors connected in parallel have the same potential. The potential across the wire is the same at all points and changes when an element is connected in between. Two points coincide if they have the same potential.