Question

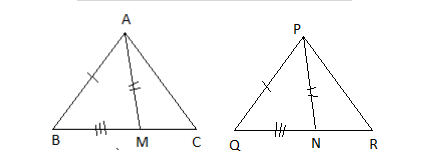
In the given figures, two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of\[\vartriangle PQR\]. Show that:
I.\[\vartriangle ABM \cong \vartriangle PQN\]
II.\[\vartriangle ABC \cong \vartriangle PQR\]

Answer 1

Hint: The median of a triangle divides the triangles in two triangles with equal areas. A triangle is a polygon with three edges and three vertices, which are the basic shapes in geometry. It is a closed two-dimensional shape with three straight sides.
A triangle has three sides, and their type depends on the length of its sides and the size of its angles. There are basically three types of a triangle based on the length of the sides, namely: Scalene Triangle, Isosceles Triangle, and Equilateral Triangle.
This question shows that the two triangles are congruent by proving corresponding sides and angles to be equal.

Complete step-by-step answer:
Given the sides
\[
  AB = PQ - - (i) \\
  AM = PN - - (ii) \\
  BC = QR - - (iii) \\
 \]
AM is the median in the\[\vartriangle ABC\]since a median divides a triangle into two congruent triangles hence we can say
 \[BM = CM = \dfrac{1}{2}BC\]
 Also, PN is the median in the\[\vartriangle PQR\],
 \[QN = RN = \dfrac{1}{2}QR\]
\[\vartriangle ABM \cong \vartriangle PQN\]
Since \[BC = QR\]already given, we can say
 \[
  \dfrac{1}{2}BC = \dfrac{1}{2}QR \\
  BM = QN - - - (iv) \\
 \]
 Now in \[\vartriangle ABM\]and \[\vartriangle PQN\]
  \[AB = PQ - - (i)\]
  \[AM = PN - - (ii)\]
  \[BM = QN - - - (iv)\]
   Hence we can say \[\vartriangle ABM \cong \vartriangle PQN\]
   Hence proved
\[\vartriangle ABC \cong \vartriangle PQR\]
Since we have already proved\[\vartriangle ABM \cong \vartriangle PQN\], so we can say
\[\angle B = \angle Q - - (iv)\](CPCT)
Now in \[\vartriangle ABM\]and \[\vartriangle PQN\]
\[AB = PQ - - (i)\]
\[\angle B = \angle Q - - (iv)\]
\[BC = QR\][Given]
Hence we can say
\[\vartriangle ABC \cong \vartriangle PQR\][By SAS congruence rule]
Hence proved

Note: Students must note that to prove two triangles congruent, they must fulfill three conditions either by providing three sides congruent or three angels to be congruent or by two sides and one angle or by two angles and one side congruent.