Question

In the given figures, the directed lines are parallel to each other. Find the unknown angles.

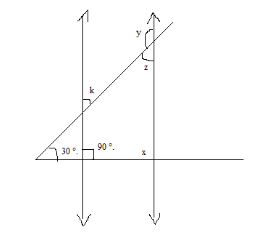
Answer 1

Hint: Here we will use the property of two parallel lines which states that if two lines are parallel and cut by a transversal then the pair of corresponding angles, interior angles, and exterior angles are equal. Also, interior angles on the same side of the transversal are supplementary.

Complete step-by-step solution:
Step 1: In the below figure, angle \[x\] and
\[\angle 1\] are co-interior angles. So, as per the property of parallel lines the sum of these two angles will be equals to \[{180^\circ}\] as shown below:

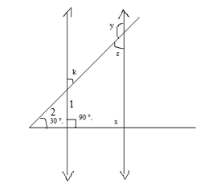
\[\angle x + \angle 1 = {180^\circ}\]
By substituting the value of \[\angle 1 = {90^\circ}\] (as given) in the above equation, we get:
\[ \Rightarrow \angle x + {90^\circ} = {180^\circ}\]
By bringing
\[{90^\circ}\] into the RHS side of the equation and subtracting it from \[{180^\circ}\] we get:
\[ \Rightarrow \angle x = {90^\circ}\]
Step 2: Now, angle
\[x\],
\[\angle 2\] and \[z\] are three angles of the triangle. And we know that the sum of the angle of the triangle is
\[{180^\circ}\]. So, we can write the equation as below:
 \[ \Rightarrow \angle x + \angle z + \angle 2 = {180^\circ}\]
By substituting the values of
\[\angle x = {90^\circ}\] and \[\angle 2 = {30^\circ}\] (as given) in the above equation we get:
\[ \Rightarrow {90^\circ} + \angle z + {30^\circ} = {180^\circ}\]
After adding the angles in the LHS side of the above equation, we get:
\[ \Rightarrow {120^\circ} + \angle z = {180^\circ}\]
By bringing
\[{120^\circ}\] into the RHS side of the equation and subtracting it from \[{180^\circ}\] we get:
\[ \Rightarrow \angle z = {60^\circ}\]
Step 3: Now, we know that any sum of the angles in any straight line always equals to
\[{180^\circ}\] , by using this property we can write the below equation:
\[ \Rightarrow \angle y + \angle z = {180^\circ}\]
By substituting the value of \[\angle z\] in the above equation we get:
\[ \Rightarrow \angle y + {60^\circ} = {180^\circ}\]
Bringing
\[{60^\circ}\] into the RHS side of the equation and subtracting it from \[{180^\circ}\] we get:
\[ \Rightarrow \angle y = {120^\circ}\]
Step 4: Angle
\[k\] and \[y\] are co-interior angles. So, as per the property of parallel lines the sum of these two angles will be equals to
\[{180^\circ}\] as shown below:
\[ \Rightarrow \angle y + \angle k = {180^\circ}\]
By substituting the value of
\[\angle y\] in the above equation we get:
\[ \Rightarrow \angle k + {120^\circ} = {180^\circ}\]
Bringing
\[{120^\circ}\] into the RHS side of the equation and subtracting it from \[{180^\circ}\] we get:
\[ \Rightarrow \angle k = {60^\circ}\]

The value of all unknown angles are \[\angle k = {60^\circ}\],
\[\angle y = {120^\circ}\],\[\angle z = {60^\circ}\] and \[\angle x = {90^\circ}\].

Note: Students need to remember the property of parallel lines while calculating the angles made by the transversal line which cuts the two parallel lines. For example:

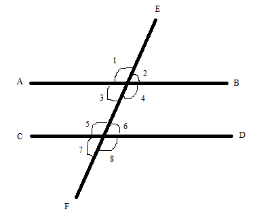
\[{\text{AB}}\] and \[{\text{CD}}\] are two parallel lines cuts by a transversal line \[{\text{EF}}\]than below are the important points to remember:
Interior and exterior alternate angles are equal. i.e. \[\angle 3 = \angle 6\], \[\angle 4 = \angle 5\](Interior angles)
\[\angle 1 = \angle 8\] and
\[\angle 2 = \angle 7\](exterior angles)
Corresponding angles of the lines are equal, i.e. \[\angle 2 = \angle 6\], \[\angle 1 = \angle 5\], \[\angle 3 = \angle 7\] and \[\angle 4 = \angle 8\]
Co-interior angles are supplementary, i.e. \[\angle 3 + \angle 5 = {180^\circ}\] and \[\angle 4 + \angle 6 = {180^\circ}\].