Question

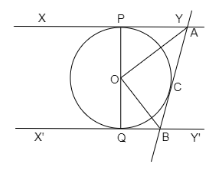
In the given figure, XY and X’Y’ are two parallel tangents to a circle with center O and another tangent AC with the point of contact C intersects XY at A and X’Y’ at B. Prove that $\angle AOB = 90^\circ $.

Answer 1

Hint: Tangent at any point of a circle is perpendicular to the radius through the point of contact. First, take two triangles OPA and OCA, and show that they are congruent. Then use the properties of congruence and two parallel lines with a traversal to prove it.

Complete step-by-step answer:
CIRCLE: Circle is defined as the locus of a point which moves in a plane such that its distance from a fixed point in that plane is constant.
TANGENT: In geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior
CONGRUENCE OF TRIANGLES: Two triangles that are identical in all respects are said to be congruent and are denoted by the symbol. . In two congruent triangles,
The corresponding sides are equal.
The corresponding angles are equal.
As we already know that tangent to a circle is perpendicular to the radius of the circle at the point of contact.
Join O at C.

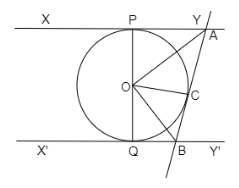
\[ \Rightarrow OP \bot XY\]
\[ \Rightarrow OC \bot AB\]
Now, in $\Delta OPA$ and $\Delta OCA$,
$ \Rightarrow \angle OPA = \angle OCA$ (Angles with tangents and radius is $90^\circ $ )
$ \Rightarrow OP = OC$ (radii)
$ \Rightarrow AP = AC$ (Length of tangents from an external point are equal)
By SAS congruence criteria,
$\Delta OPC \cong \Delta OCA$
By CPCT,
$ \Rightarrow \angle OAC = \angle OAC$
Then, the value of \[\angle OAC\] in terms of \[\angle PAC\],
$ \Rightarrow \angle OAC = \dfrac{1}{2}\angle PAC$.............….. (1)
Similarly, we can also say that,
\[ \Rightarrow \angle OBC = \angle OBQ\]
Then, the value of \[\angle OBC\] in terms of \[\angle QBC\],
$ \Rightarrow \angle OBC = \dfrac{1}{2}\angle QBC$...........….. (2)
As we know that XY and X'Y' are parallel. So, here AB acts as a transversal.
\[ \Rightarrow \angle PAC + \angle QBC = 180^\circ \] (sum of interior angles)
Divide both sides by 2,
\[ \Rightarrow \dfrac{1}{2}\angle PAC + \dfrac{1}{2}\angle QBC = 90^\circ \]
Substitute the values from equation (1) and (2),
$ \Rightarrow \angle OAC + \angle OBC = 90^\circ $.........….. (3)
From $\Delta OAB$, we can write,
\[ \Rightarrow \angle AOB + \angle OAB + \angle OBA = 180^\circ \]
Substitute the values from equation (3),
$ \Rightarrow \angle AOB + 90^\circ = 180^\circ $
Move $90^\circ $ to the other side and subtract,
$\therefore \angle AOB = 90^\circ $
Hence, it is proved.

Note: In order to prove the congruence, you need to look at all the sides and angles which are equal because neglecting one of them changes the rule of congruence.
As we know that the line joining the center and the external point from where tangents are drawn to the circle bisects the angle formed at the external point to the circle.