Question

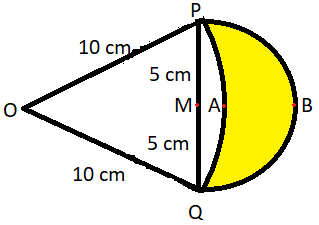
In the given figure two areas POQ and PBQ are shown. Arc PAQ is a part of the circle with center O and the radius OP while PBQ is semicircle drawn on PQ as diameter with center M. IF OP = PQ = 10cm, that area of shaded region is $\dfrac{{25\left( {6\sqrt k - \pi } \right)}}{6}$, the k =

Answer 1

Hint: In this particular question use the concept that the area of the shaded region = area of the semicircle PBQ - (area of sector OPAQO – area of equilateral triangle OPQ) and use that the tangent drawn from the external fixed point on the circle is always equal so use these concepts to reach the solution of the question.

Complete step by step answer:
Given data:
OP = PQ = 10 cm.
MP = MQ = 5 cm.
As we know that the tangent drawn from the external fixed point on the circle is always equal.
So OP = OQ = 10
Therefore, OP = OQ = PQ = 10cm.
Therefore, OPQ is an equilateral triangle.
Now as we know that the area of the semicircle is = $\dfrac{1}{2}\pi {r^2}$, where r is the radius of the semicircle.
Now as we know that the radius is half of the diameter (d)
Therefore, r = (d/2)
So the area $\left( {{A_1}} \right)$ of the semicircle = $\dfrac{1}{2}\pi {\left( {\dfrac{d}{2}} \right)^2} = \dfrac{1}{8}\pi {d^2}$
Now PQ is the diameter of the semicircle PBQ.
Therefore, PQ = d = 10cm
So the area $\left( {{A_3}} \right)$ of the semicircle = $ = \dfrac{1}{8}\pi {\left( {10} \right)^2} = \dfrac{{100\pi }}{8} = \dfrac{{25\pi }}{2}$ square cm
Now we know that the area (${A_2}$) of the equilateral triangle is given as square root 3 divided by 4 and whole multiplied by side square.
Therefore, ${A_2} = \dfrac{{\sqrt 3 }}{4}{\left( {OP} \right)^2} = \dfrac{{\sqrt 3 }}{4}{\left( {10} \right)^2} = 25\sqrt 3 $ square cm.
Now it is given that OPAQO is a part of a circle.
So the area corresponding to this sector is the ratio of the angle subtended by the PQ on the center of the circle to the total angle at the center of the circle, multiplied by the area of the circle.
As triangle OPQ is an equilateral triangle therefore, angle subtended at the center = ${60^o}$ (as all the angles in an equilateral triangle is equal to ${60^o}$).
And the whole angle at the center = ${360^o}$
And we all know that the area of the circle is $\pi {r^2}$, where r is the radius of the circle.
So the area (${A_3}$) corresponding to the sector OPAQO = $\dfrac{{{{60}^o}}}{{{{360}^o}}}\left( {\pi {r^2}} \right)$
Now the radius of the circle is given, OP = r = 10cm.
Therefore, ${A_3} = \dfrac{{{{60}^o}}}{{{{360}^o}}}\left( {\pi {r^2}} \right) = \dfrac{1}{6}\left( {\pi {{\left( {10} \right)}^2}} \right) = \dfrac{{100\pi }}{6} = \dfrac{{50\pi }}{3}$ square cm.
So the area of the shaded region = area of the semicircle PBQ – area of segment PAQMP.
But area of PAQMP is = (area of the sector OPAQO – area of the equilateral triangle).
So the area of the shaded region = area of the semicircle PBQ – (area of the sector OPAQO – area of the equilateral triangle)
Therefore,
So the area of the shaded region = ${A_1} - \left( {{A_3} - {A_2}} \right) = {A_1} - {A_3} + {A_2}$
So the area of the shaded region = $\dfrac{{25\pi }}{2} - \dfrac{{50\pi }}{3} + 25\sqrt 3 $
Now simplify this we have,
So the area of the shaded region = $25\sqrt 3 - \dfrac{{25\pi }}{6} = \dfrac{{25\left( {6\sqrt 3 - \pi } \right)}}{6}$ square cm.
So on comparing with given area we have,
$ \Rightarrow \dfrac{{25\left( {6\sqrt k - \pi } \right)}}{6} = \dfrac{{25\left( {6\sqrt 3 - \pi } \right)}}{6}$
So on comparing, k = 3.
So this is the required answer.

Note: Whenever we face such types of question the key concept we have to remember is that the area corresponding to the sector (OPAQO) is the ratio of the angle subtended by the PQ on the center of the circle to the total angle at the center of the circle whole multiplied by the area of the circle and always recall the area of the circle and the semicircle in radius form as well as in diameter form which is all stated above.