Question

In the given figure the value of x is?

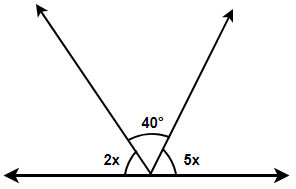
(a) ${{30}^{\circ }}$
(b) ${{10}^{\circ }}$
(c) ${{20}^{\circ }}$
(d) ${{40}^{\circ }}$

Answer 1

Hint: Consider the horizontal line as a straight line and use the fact that ‘the sum of all the angles formed on a straight line is equal to 180 degrees’. Add the three angles and equate them with 180 degrees to form a linear expression in x. Solve for the value of x to get the answer.

Complete step by step answer:
Here we have been provided with the figure shown below where we have three angles formed on a straight line and we are asked to find the value of x.

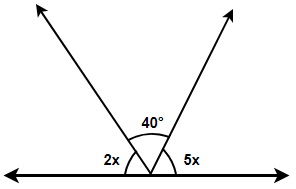
Now, we know that the angle of a straight line is equal to 180 degrees. So if we form several angles on a straight line then their sum must be equal to the total measure of the angle of the straight line, i.e. 180 degree. In the figure we have three angles formed on the horizontal straight line, so we get,
$\begin{align}
  & \Rightarrow 2x+{{40}^{\circ }}+5x={{180}^{\circ }} \\
 & \Rightarrow 7x={{140}^{\circ }} \\
 & \therefore x=20 \\
\end{align}$
So, the correct answer is “Option c”.

Note: Note that you can roughly say that the three angles are forming a linear pair, although they are not a pair because a pair contains two angles. If you combine two angles to consider them as a single unit and leave the third one alone then you can say they are a linear pair. The sum of angles in a linear pair is always equal to 180 degrees hence they can be called a supplementary angle, however the converse is not true.