
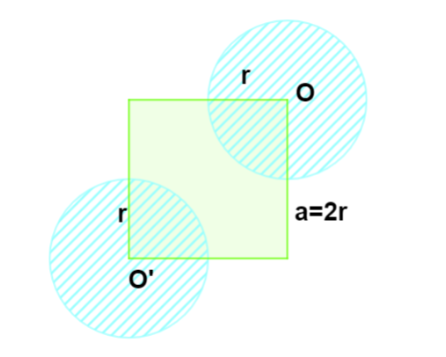
In the given figure, the side of the square is

Answer
481.5k+ views
Hint: The given geometric figure deals with the shapes called circle and square. We will use the area formulas of these shapes to find the area of the required portion. More precisely we will add the area of the circles and square and then subtract the part that occurred twice.
Formula used:
1) The area of a square of side
2) The area of a circle of radius
Complete step-by-step answer:
The given figure has a square of side
Let
Let the radius of the circle with Centre
According to the question the radius of the two circles is half of the side of the square.
So,
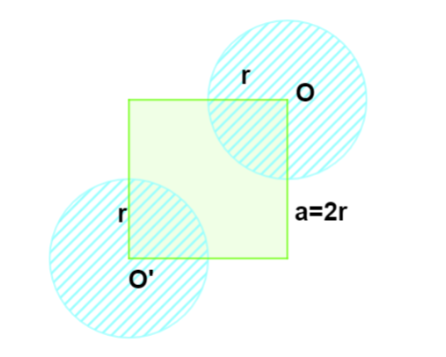
Let
Now from the formulas of area of these geometric shapes we have:
Adding all the above we get total area
The area we have calculated adds the area common between the two circles and square.
From the figure we can see that the extra added area is
So we have to subtract it from the generated area in order to find the required area.
Now, the required area becomes
From (1) we have
So, the correct answer is “ 1707.16
Note: The area common between the circle two circles and the square will give an area greater than the area of the colored region. To avoid this we have to subtract the repeated area while calculating the required shaded area. Don’t forget to put the unit of the area after calculating it, in our case it is
Formula used:
1) The area of a square of side
2) The area of a circle of radius
Complete step-by-step answer:
The given figure has a square of side
Let
Let the radius of the circle with Centre
According to the question the radius of the two circles is half of the side of the square.
So,

Let
Now from the formulas of area of these geometric shapes we have:
Adding all the above we get total area
The area we have calculated adds the area common between the two circles and square.
From the figure we can see that the extra added area is
So we have to subtract it from the generated area in order to find the required area.
Now, the required area becomes
From (1) we have
So, the correct answer is “ 1707.16
Note: The area common between the circle two circles and the square will give an area greater than the area of the colored region. To avoid this we have to subtract the repeated area while calculating the required shaded area. Don’t forget to put the unit of the area after calculating it, in our case it is
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What is pollution? How many types of pollution? Define it




