Question

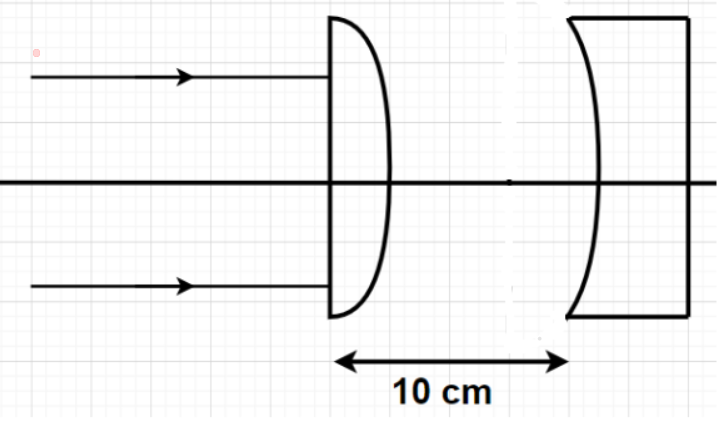
In the given figure, the radius of curvature of a curved surface for both the piano-convex and plano-concave lens is 10 cm and the refractive index for both is 1.5. What is the location of the final image after all the refractions through lenses?

${\text{A}}{\text{.}}$ 15 cm
${\text{B}}{\text{.}}$ 20 cm
${\text{C}}{\text{.}}$ 25 cm
${\text{D}}{\text{.}}$ 40 cm

Answer 1

Hint: Here, we will proceed by using the lens maker equation to find the focal lengths of the given lenses. Then, we will find the final image distance after refraction through both the lenses.
Formulas Used- $\dfrac{1}{{\text{f}}} = \left( {{\text{n}} - 1} \right)\left( {\dfrac{1}{{{{\text{R}}_2}}} - \dfrac{1}{{{{\text{R}}_1}}}} \right)$ and $\dfrac{1}{{\text{f}}} = \dfrac{1}{{\text{v}}} - \dfrac{1}{{\text{u}}}$.

Complete Step-by-Step solution:
Let us suppose that all the distances measured in the right direction from the poles are taken as positive whereas all the distances measured in the left direction from the poles are taken as negative.
According to lens maker’s equation if the lens is placed in air as the surrounding medium (i.e., Refractive index of air/surrounding = 1), we can write
$\dfrac{1}{{\text{f}}} = \left( {{\text{n}} - 1} \right)\left( {\dfrac{1}{{{{\text{R}}_2}}} - \dfrac{1}{{{{\text{R}}_1}}}} \right){\text{ }} \to {\text{(1)}}$ where f denotes the focal length of the lens, n denotes the refractive index of the lens material, ${{\text{R}}_1}$ denotes the radius of curvature for the surface on which light is incident upon, ${{\text{R}}_2}$ denotes the radius of curvature for the surface from which light is exiting through.
For the given piano-convex lens,
Refractive index of lens material n = 1.5 (Given)
Radius of curvature for the surface on which light is incident upon ${{\text{R}}_1} = \infty $
 Radius of curvature for the surface from which light is exiting through ${{\text{R}}_2}$ = 10 cm (Given)
Using the formula given by equation (1), focal length for the piano-convex lens is given by
$
  \dfrac{1}{{\text{f}}} = \left( {{\text{1}}{\text{.5}} - 1} \right)\left( {\dfrac{1}{{10}} - \dfrac{1}{\infty }} \right) = 0.5\left( {\dfrac{1}{{10}} - 0} \right) = \dfrac{{0.5}}{{10}} = \dfrac{5}{{10 \times 10}} = \dfrac{1}{{20}} \\
   \Rightarrow {\text{f}} = 20{\text{ cm}} \\
 $
So, the focal length for the piano-convex lens is 20 cm
For the given plano-concave lens,
Refractive index of lens material n = 1.5 (Given)
Radius of curvature for the surface on which light is incident upon ${{\text{R}}_1} = 10$ cm (Given)
Radius of curvature for the surface from which light is exiting through ${{\text{R}}_2} = \infty $
Using the formula given by equation (1), focal length for the plano-concave lens is given by
$
  \dfrac{1}{{\text{f}}} = \left( {{\text{1}}{\text{.5}} - 1} \right)\left( {\dfrac{1}{\infty } - \dfrac{1}{{10}}} \right) = 0.5\left( {0 - \dfrac{1}{{10}}} \right) = - \dfrac{{0.5}}{{10}} = - \dfrac{5}{{10 \times 10}} = - \dfrac{1}{{20}} \\
   \Rightarrow {\text{f}} = - 20{\text{ cm}} \\
 $
So, the focal length for the plano-concave lens is -20 cm
According to lens formula, we can write
$\dfrac{1}{{\text{f}}} = \dfrac{1}{{\text{v}}} - \dfrac{1}{{\text{u}}}{\text{ }} \to {\text{(2)}}$ where f denotes the focal length of the lens, v denotes the distance of the image formed from the pole of the lens, u denotes the object distance measured from the pole of lens
By substituting f = 20 cm and u = $\infty $ (since both the incident rays are parallel and hence the object is placed at infinity) for given piano-convex lens in equation (2), we get
..
So, the image for the plano-convex lens which is actually the object for the plano-concave lens will be formed at 20 cm in the right direction from the pole of the plano-convex lens. Since, the distance between the two lenses is 10 cm. So, the object distance for plano-concave lens is +10 cm
By substituting f = -20 cm and u = 10 cm for given plano-concave lens in equation (2), we get
$
   \Rightarrow \dfrac{1}{{ - 20}} = \dfrac{1}{{\text{v}}} - \dfrac{1}{{10}} \\
   \Rightarrow \dfrac{1}{{\text{v}}} = \dfrac{1}{{{\text{10}}}} - \dfrac{1}{{{\text{20}}}} \\
   \Rightarrow \dfrac{1}{{\text{v}}} = \dfrac{{2 - 1}}{{{\text{20}}}} \\
   \Rightarrow \dfrac{1}{{\text{v}}} = \dfrac{1}{{{\text{20}}}} \\
   \Rightarrow {\text{v}} = 20{\text{ cm}} \\
 $
Therefore, the final image after all the refractions through lenses is located at 20 cm
Hence, option B is correct.

Note- As the radius of curvature for any plane surface is always infinite. In this particular problem, ${{\text{R}}_1}$ and ${{\text{R}}_2}$ for piano-convex lens represents the radius of curvature for plane surface and that for curved surface respectively. Also, ${{\text{R}}_1}$ and ${{\text{R}}_2}$ for plano-concave lens represents the radius of curvature for curved surface and that for plane surface respectively.