
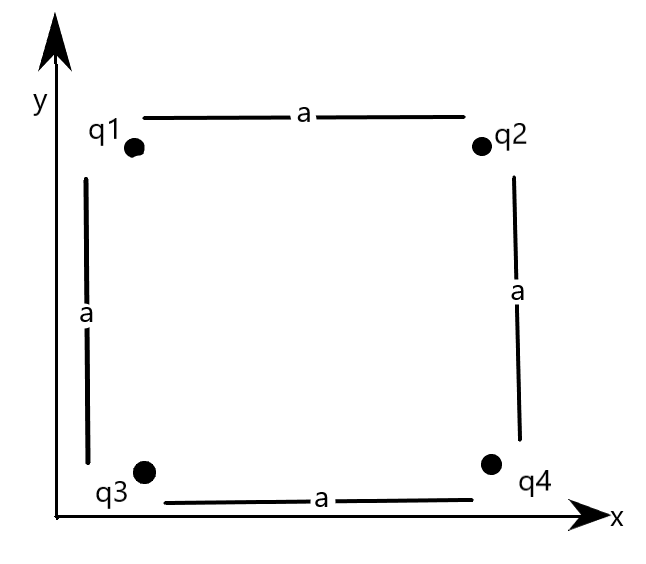
In the given figure, the particles have charge, \[{{q}_{1}}=-{{q}_{2}}=100nC\text{ }\]\[\text{and }{{q}_{3}}=-{{q}_{4}}=200nC\],and if the distance, \[a=5.0cm\]. What are the x components of force?

Answer
567.6k+ views
Hint: We can find the force due to a combination of static charges by comparing the forces due to each pair of the charges. Here, we are to find the force along the x-component of the setup. We can consider this by taking one of the charges into account.
Complete answer:
We are given four charges arranged in the corners of a square of side ‘a’. We have to find the x-component of electric force due to this arrangement. In order to do that, we have to consider one of the charges on which the forces act due to other charges. We know that taking the charge on the x-axis will make our approach easier.
Let us consider \[{{q}_{3}}\]as the central charge. Now, we can find the force on a charge ‘q’ due to another charge ‘Q’ at distance ‘r’ is given by –
\[{{F}_{e}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{qQ}{{{r}^{2}}}\]
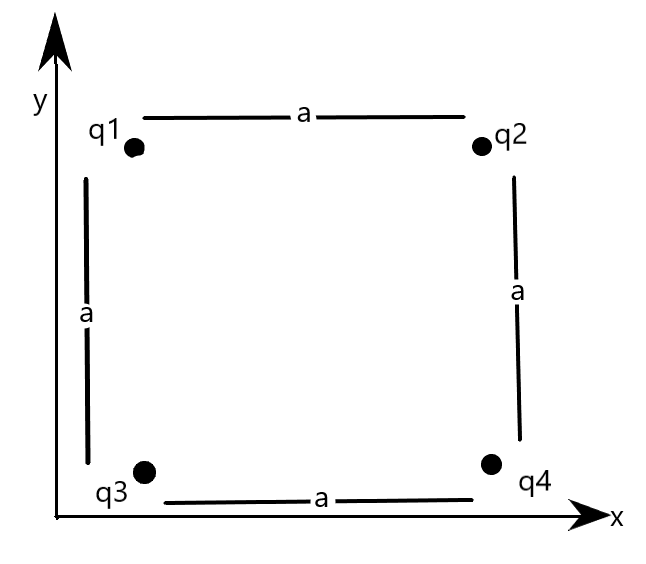
Now, let us consider the given situation of charges.
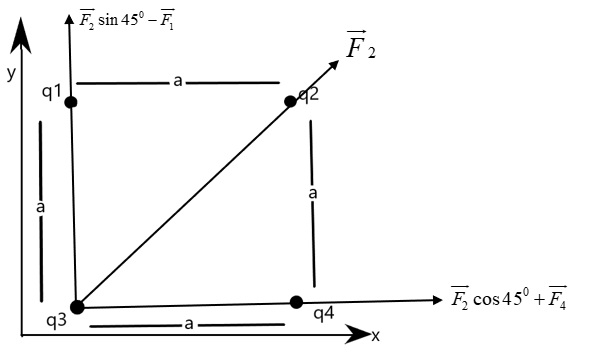
Let us consider the forces on the charge \[{{q}_{3}}\] due to the other charges using vector algebra –
\[\begin{align}
& {{F}_{e}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{qQ}{{{r}^{2}}} \\
& {{\overrightarrow{F}}_{3}}={{\overrightarrow{F}}_{1}}+{{\overrightarrow{F}}_{2}}+{{\overrightarrow{F}}_{4}} \\
& {{\overrightarrow{F}}_{3}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{3}}}{{{a}^{2}}}(-\widehat{j})+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{3}}{{q}_{2}}}{{{(\sqrt{2}a)}^{2}}}(\cos {{45}^{0}}i+\sin {{45}^{0}}\widehat{j})+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{3}}{{q}_{4}}}{{{a}^{2}}}\widehat{i} \\
\end{align}\]
Let us now, consider the x-components of force. All the force components with the vector ‘i’ counts to be the x-components. So, let us group them as –
\[\begin{align}
& \overrightarrow{{{F}_{3x}}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{3}}{{q}_{2}}}{{{(\sqrt{2}a)}^{2}}}(\cos {{45}^{0}}i)+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{3}}{{q}_{4}}}{{{a}^{2}}}\widehat{i} \\
& \Rightarrow \text{ }\overrightarrow{{{F}_{3x}}}=\dfrac{{{q}_{3}}}{4\pi {{\varepsilon }_{0}}}[\dfrac{{{q}_{4}}}{{{a}^{2}}}\widehat{i}+\dfrac{{{q}_{2}}}{{{(\sqrt{2}a)}^{2}}}(\cos {{45}^{0}})] \\
\end{align}\]
Now, we can substitute the values of the charges as given –
\[\begin{align}
& \overrightarrow{{{F}_{3x}}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{3}}{{q}_{2}}}{{{(\sqrt{2}a)}^{2}}}(\cos {{45}^{0}}i)+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{3}}{{q}_{4}}}{{{a}^{2}}}\widehat{i} \\
& {{q}_{1}}=-{{q}_{2}}=100nC\text{ } \\
& {{q}_{3}}=-{{q}_{4}}=200nC \\
& \text{and,} \\
& a=5.0cm \\
\end{align}\]
\[\begin{align}
& \Rightarrow \text{ }\left| \overrightarrow{{{F}_{3x}}} \right|=\dfrac{{{q}_{3}}}{4\pi {{\varepsilon }_{0}}}[\dfrac{{{q}_{4}}}{{{a}^{2}}}\widehat{i}+\dfrac{{{q}_{2}}}{{{(\sqrt{2}a)}^{2}}}(\cos {{45}^{0}})] \\
& \Rightarrow \text{ }\left| \overrightarrow{{{F}_{3x}}} \right|=200\times {{10}^{-9}}\times 9\times {{10}^{9}}[\dfrac{200\times {{10}^{-9}}}{{{(5\times {{10}^{-2}})}^{2}}}+\dfrac{200\times {{10}^{-9}}}{{{(\sqrt{2}\times 5\times {{10}^{-2}})}^{2}}}(\dfrac{1}{\sqrt{2}})] \\
& \Rightarrow \text{ }\left| \overrightarrow{{{F}_{3x}}} \right|=1800\times [\dfrac{200\times {{10}^{-9}}}{25\times {{10}^{-4}}}+\dfrac{200\times {{10}^{-9}}}{50\sqrt{2}\times {{10}^{-4}}}] \\
& \Rightarrow \text{ }\left| \overrightarrow{{{F}_{3x}}} \right|=0.19N \\
\end{align}\]
So, the force along the x-axis is approximately 0.2N. This is the required solution for the given data.
Note:
We can either use the vector calculation as we did here, or can consider the signs of the charge while substitution in the formula. You should be careful not to consider the force direction beforehand and again apply the charges in the substitution.
Complete answer:
We are given four charges arranged in the corners of a square of side ‘a’. We have to find the x-component of electric force due to this arrangement. In order to do that, we have to consider one of the charges on which the forces act due to other charges. We know that taking the charge on the x-axis will make our approach easier.
Let us consider \[{{q}_{3}}\]as the central charge. Now, we can find the force on a charge ‘q’ due to another charge ‘Q’ at distance ‘r’ is given by –
\[{{F}_{e}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{qQ}{{{r}^{2}}}\]

Now, let us consider the given situation of charges.

Let us consider the forces on the charge \[{{q}_{3}}\] due to the other charges using vector algebra –
\[\begin{align}
& {{F}_{e}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{qQ}{{{r}^{2}}} \\
& {{\overrightarrow{F}}_{3}}={{\overrightarrow{F}}_{1}}+{{\overrightarrow{F}}_{2}}+{{\overrightarrow{F}}_{4}} \\
& {{\overrightarrow{F}}_{3}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{3}}}{{{a}^{2}}}(-\widehat{j})+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{3}}{{q}_{2}}}{{{(\sqrt{2}a)}^{2}}}(\cos {{45}^{0}}i+\sin {{45}^{0}}\widehat{j})+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{3}}{{q}_{4}}}{{{a}^{2}}}\widehat{i} \\
\end{align}\]
Let us now, consider the x-components of force. All the force components with the vector ‘i’ counts to be the x-components. So, let us group them as –
\[\begin{align}
& \overrightarrow{{{F}_{3x}}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{3}}{{q}_{2}}}{{{(\sqrt{2}a)}^{2}}}(\cos {{45}^{0}}i)+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{3}}{{q}_{4}}}{{{a}^{2}}}\widehat{i} \\
& \Rightarrow \text{ }\overrightarrow{{{F}_{3x}}}=\dfrac{{{q}_{3}}}{4\pi {{\varepsilon }_{0}}}[\dfrac{{{q}_{4}}}{{{a}^{2}}}\widehat{i}+\dfrac{{{q}_{2}}}{{{(\sqrt{2}a)}^{2}}}(\cos {{45}^{0}})] \\
\end{align}\]
Now, we can substitute the values of the charges as given –
\[\begin{align}
& \overrightarrow{{{F}_{3x}}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{3}}{{q}_{2}}}{{{(\sqrt{2}a)}^{2}}}(\cos {{45}^{0}}i)+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{3}}{{q}_{4}}}{{{a}^{2}}}\widehat{i} \\
& {{q}_{1}}=-{{q}_{2}}=100nC\text{ } \\
& {{q}_{3}}=-{{q}_{4}}=200nC \\
& \text{and,} \\
& a=5.0cm \\
\end{align}\]
\[\begin{align}
& \Rightarrow \text{ }\left| \overrightarrow{{{F}_{3x}}} \right|=\dfrac{{{q}_{3}}}{4\pi {{\varepsilon }_{0}}}[\dfrac{{{q}_{4}}}{{{a}^{2}}}\widehat{i}+\dfrac{{{q}_{2}}}{{{(\sqrt{2}a)}^{2}}}(\cos {{45}^{0}})] \\
& \Rightarrow \text{ }\left| \overrightarrow{{{F}_{3x}}} \right|=200\times {{10}^{-9}}\times 9\times {{10}^{9}}[\dfrac{200\times {{10}^{-9}}}{{{(5\times {{10}^{-2}})}^{2}}}+\dfrac{200\times {{10}^{-9}}}{{{(\sqrt{2}\times 5\times {{10}^{-2}})}^{2}}}(\dfrac{1}{\sqrt{2}})] \\
& \Rightarrow \text{ }\left| \overrightarrow{{{F}_{3x}}} \right|=1800\times [\dfrac{200\times {{10}^{-9}}}{25\times {{10}^{-4}}}+\dfrac{200\times {{10}^{-9}}}{50\sqrt{2}\times {{10}^{-4}}}] \\
& \Rightarrow \text{ }\left| \overrightarrow{{{F}_{3x}}} \right|=0.19N \\
\end{align}\]
So, the force along the x-axis is approximately 0.2N. This is the required solution for the given data.
Note:
We can either use the vector calculation as we did here, or can consider the signs of the charge while substitution in the formula. You should be careful not to consider the force direction beforehand and again apply the charges in the substitution.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




