Question

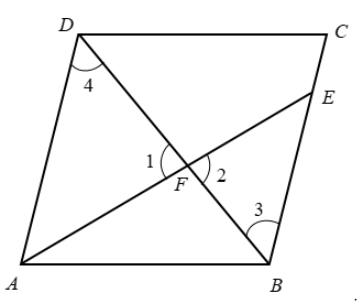
In the given figure, the diagonal \[BD\] of a parallelogram \[ABCD\] intersects the segment \[AE\] at the point \[F\], where \[E\] is any point on the side \[BC\]. Prove that \[DF \times EF = FB \times FA\].

Answer 1

Hint:
Here, we will prove the given equation by proving the two triangles are similar using the AA similarity criterion. According to the AA similarity criterion, two triangles are similar if any two corresponding angles are equal.

Complete step by step solution:
We can observe that \[DF\] and \[FA\] are sides of the triangle \[DFA\].
Also, \[FB\] and \[EF\] are sides of the triangle \[BFE\].
We know that the opposite sides of a parallelogram are equal and parallel.
Therefore, the sides \[BC\] and \[AD\] are parallel to each other.
Now, we know that the alternate interior angles on opposite sides of a transversal between two parallel lines are equal.
The diagonal \[BD\] is the transversal between the parallel lines \[BC\] and \[AD\].
Therefore, we get
\[\begin{array}{l}\angle ADF = \angle EBF\\ \Rightarrow \angle 4 = \angle 3\end{array}\]
Next, we know that the vertically opposite angles formed at the intersection of two straight lines are equal.
Therefore, we get
\[\begin{array}{l}\angle DFA = \angle BFE\\ \Rightarrow \angle 1 = \angle 2\end{array}\]
Now, we will prove that the triangles \[DFA\] and \[BFE\] are similar.
In triangles \[DFA\] and \[BFE\], we have
\[\angle 4 = \angle 3\]
\[\angle 1 = \angle 2\]
According to the AA similarity criterion, two triangles are similar if any two corresponding angles are equal.
Therefore, by the AA similarity criterion, the triangles \[DFA\] and \[BFE\] are similar.
Now, we know that the corresponding sides of two similar triangles are in equal ratio.
Therefore, we get
\[\dfrac{{DF}}{{BF}} = \dfrac{{FA}}{{FE}} = \dfrac{{DA}}{{BE}}\]
Thus, we have
\[ \Rightarrow \dfrac{{DF}}{{BF}} = \dfrac{{FA}}{{FE}}\]
Simplifying the equation, we get
\[ \Rightarrow DF \times FE = BF \times FA\]
\[\therefore DF\times EF=FB\times FA\]
Hence, the equation is proved.

Note:
Note: Here, we need to know the different conditions for two triangles to be equal. There are four criteria that a pair of triangles must follow to be similar. If any of the conditions proves to be true, then the two triangles are similar.
1) AAA Similarity criterion
According to this criterion, if the corresponding angles of the two triangles are equal, then the two triangles are similar.
2) AA Similarity criterion
According to this criterion, if any two corresponding angles of two triangles are equal, then the two triangles are similar.
The third angle of the two triangles will also be equal since the sum of angles of a triangle is always 180 degrees.
Hence, if two of the angles of the triangles are equal, then the third angle of the two triangles will also be equal.
3) SSS Similarity criterion
According to this criterion, if the corresponding sides of the two triangles are in the same ratio, then the two triangles are similar.
4) SAS Similarity criterion
According to this criterion, if one corresponding angle of the two triangles is equal, and the corresponding sides of the two triangles that form the equal angle are in the same ratio, then the two triangles are similar.