Question

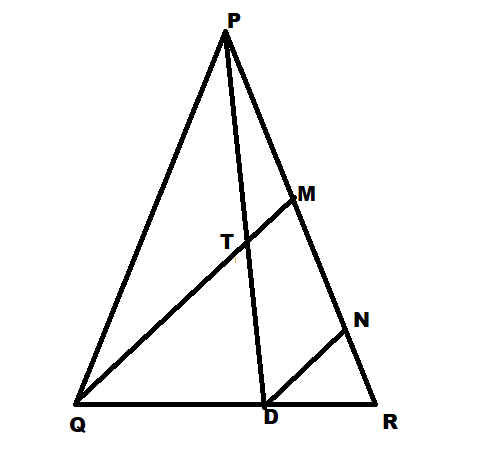
In the given figure, segment PD is a median of triangle PQR point T is the midpoint of segment
PD. Produced QT intersect PR at M. Show that PM/PR=1/3 [Hint: draw DN||QM]

Answer 1

Hint: Here we are to prove a condition with the given data for the triangle, for such question we have to search for the best suited approach it may any formulae or standard proven property for the triangle, then by using that we just have to but the values given in the question and reach to our final desired value which needs to be proved.

Complete step by step solution:
The given question needs to prove the given condition, on solving we get:
PD is the median of QR,
So, D is the midpoint of QR,
DN is drawn parallel to QM.
By converse of midpoint theorem, N is the midpoint of MR,
Similarly, T is the midpoint of PD
Also DN|| QM
So, by converse of midpoint of PN,
Now we obtain that, N is the midpoint of MR and T is the midpoint of PD.
On framing it to the mathematical expression we get,
\[
   \Rightarrow PM = MN = NR \\
   \Rightarrow \dfrac{{PM}}{{PR}} = \dfrac{{PM}}{{PM + PM + PM}} = \dfrac{{PM}}{{3PM}} = \dfrac{1}{3} \\
   \Rightarrow \dfrac{{PM}}{{PR}} = \dfrac{1}{3} \\
 \]
Hence now we get the desired condition asked in the question and we got the same result which finally proves the final condition asked for.

Note: Here for this question we have used the midpoint theorem of triangle which states that for any triangle the bisector extended from one vertex to front side of the triangle will divide the line into two equal parts.