Question

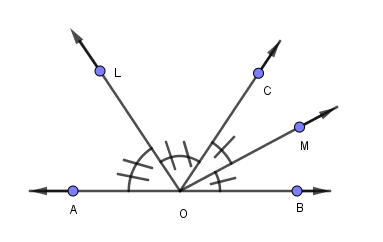
In the given figure, ray OC stands on the line AB; ray OL and ray OM are angle bisectors of $\angle AOC$ and $\angle BOC$ respectively. Find the value of $\angle LOM$.

A. ${90^ \circ }$
B. ${100^ \circ }$
C. ${180^ \circ }$
D. ${120^ \circ }$

Answer 1

Hint: Here, AOB is a straight line. So, $\angle AOB = {180^ \circ }$. From figure, $\angle AOL =\angle COL$ and $\angle BOM =\angle COM$. Add all four angles in the figure and by substitution we have only two unknown angles. Equate the sum with ${180^ \circ }$ to get the result.

Complete step by step solution:
In the given figure, $AB$ is a straight line and $OC$ is a ray stand on $AB$ at $O$.
Thus, $\angle AOC$ and $\angle BOC$ form a linear pair. Therefore the sum of these two angles is ${180^ \circ }$.
[Sum of all angles which together forms a straight line is ${180^ \circ }$ ]
i.e. $\angle AOC$+$\angle BOC$=${180^ \circ }$
Since ray $OL$ and ray $OM$ are the angle bisector of $\angle AOC$ and $\angle BOC$ respectively.
So, OL divides $\angle AOC$ into two equal parts and $OM$ divides $\angle BOC$ into two equal parts.
$\Rightarrow \angle AOL = \angle COL = \dfrac{1}{2}\angle AOC$ and $\angle BOM = \angle COM = \dfrac{1}{2}\angle BOC$
Now we have,
$\angle AOC$+$\angle BOC={180^ \circ }$


$ \Rightarrow 2\angle COL + 2\angle COM = {180^ \circ }$
As we have $\angle COL + \angle COM = \angle LOM$
$ \Rightarrow 2\angle LOM = {180^ \circ }$
$ \Rightarrow \angle LOM = {90^ \circ }$

$\therefore$ The value of $\angle LOM$$={90^\circ}$. Hence, option (A) is correct.

Note:
In these types of questions, we can geometrically analyse the answer of the questions asked. With the help of some properties and definitions we can prove it.
Some important points:
Angle bisector is the line that bisects the angle. There are three angle bisectors in a triangle. The angle bisectors of angles of a triangle meet at a point. Point at which angle bisectors of angles of a triangle meet is called in-centre of triangles. It always lies inside a triangle. In-centre is the point that is equidistant from all sides of the triangle. This distance is called the in-radius of the triangle. Thus, we can draw a circle taking in-centre and in-radius, this circle is called in-circle. If the angle bisectors of two angles of a triangle meet at a point thus angle formed by them is half of the third angle more than right angle.
Two angles form a linear pair if their sum is ${180^ \circ }$.
The angle bisectors of angles of linear pair stand at the right angle.