Question

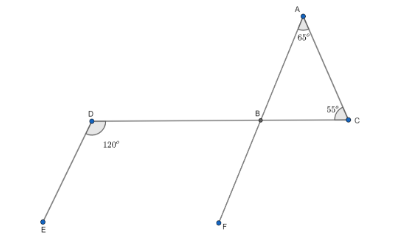
In the given figure prove that BF||DE

Answer 1

Hint:This is a question of lines and angles. We will be using various properties of triangles to prove that the two lines BF and DE are parallel. We will first apply the angle sum property in the triangle ABC to find the angle ABC. Then we will apply linear angle property, to find the angle CBF. If this is equal to the given angle BDE then the lines should be parallel.

Complete step-by-step answer:
We need to prove that BF||DE. We have been given two out of the three angles in triangle ABC. So we can apply the angle sum property which states that the sum of the angles is equal to $ {180^ \circ } $ . So-
 $ \begin{align}
  &In\;\vartriangle ABC, \\
  &\angle A + \angle B + \angle C = {180^\circ} \\
  &{65^\circ} + \angle B + {55^\circ} = {180^\circ} \\
  &\angle B = {180^\circ} - {65^\circ} - {55^\circ} \\
  &\angle B = {60^\circ} \\
\end{align} $

Now, we can see that the angles ABC and CBF lie along the same line, so their sum will be a linear angle, that is $ {180^\circ} $
 $ \begin{align}
  &\angle ABC + \angle CBF = {180^\circ} \\
  &{60^\circ} + \angle CBF = {180^\circ} \\
  &\angle CBF = {180^\circ} - {60^\circ} = {120^\circ} \\
\end{align} $
Here, we can see that the angles CBF and BDE are equal to each other. When we look closely, we can see that they are corresponding angles between the lines BF and DE. They are equal so the lines BF and DE should be parallel.
BF || DE
Hence proved.

Note: In such types of questions, we should keep in mind the definition of each type of pairs of angles. For example, we should keep in mind the definition of corresponding angles, alternate interior angles, linear angles and so on. This is because students often confuse between these definitions and end up getting the wrong answer.