Question

In the given figure, prove that $AB\parallel EF$.

.

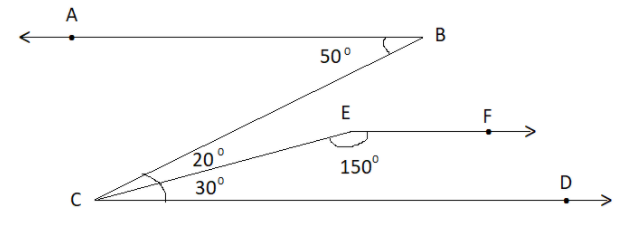
Answer 1

Hint : In this type of question, we will use the concept of transversal to parallel lines. This states that if a transversal intersects two parallel lines, then 1). Each pair of alternate interior angles is equal 2). Each pair of corresponding angles is equal and 3). Each pair of interior angles on the same side of the traversal is supplementary.

Complete step-by-step answer:
Given that,
$
  \angle ABC = {50^0} \\
  \angle BCE = {20^0} \\
  \angle ECD = {30^0} \\
  \angle CEF = {150^0} \\
$
To prove : $AB\parallel EF$.
Proof :
In the given figure,
$\angle ABC = {50^0}$ and
$
  \angle BCD = \angle BCE + \angle ECD \\
  \angle BCD = {20^0} + {30^0} \\
  \angle BCD = {50^0} \\
$
Here we can see that,
$\angle BCD = \angle ABC = {50^0}$.
But these are alternate interior angles on lines AB and CD and traversal BC.
So,
$AB\parallel CD$. …….. (i)
Now,
$\angle ECD = {30^0}$ and
$\angle CEF = {150^0}$.
Adding both of the angles, we will get
$
  \angle ECD + \angle CEF = {30^0} + {150^0} \\
  \angle ECD + \angle CEF = {180^0} \\
$
But these are co interior angles on lines CD and EF and traversal CE.
So,
$CD\parallel EF$. ……… (ii)
Now, from equations (i) and equation (ii), we can say that
$AB\parallel CD$.
Hence proved.

Note : Whenever we ask such types of questions, first we have to remember the correct figure. Then we have to find out all the details that are given in the question and in the figure. After that we will use the theorem of the transversal to parallel lines. By using that we will make some statements and then by those statements we can prove the required statement. Through this we will get the answer.