Question

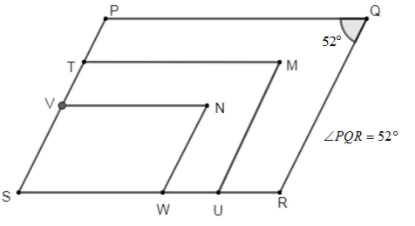
In the given figure, $PQRS$, $TMUS$ and $VNWS$ are three parallelograms. The difference between $\angle TMU$ and $\angle SVN$ is –
(a) $120{}^\circ $
(b) $64{}^\circ $
(c) $76{}^\circ $
(d) $128{}^\circ $

Answer 1

Hint: This question is based on geometrical properties and concepts of parallelogram. Here, we calculate other angles of the parallelogram by using the following properties and then we calculate the difference between $\angle TMU$ and $\angle SVN$.

Complete step-by-step solution:
(i) In any given parallelogram, opposite angles are equal, like in parallelogram $ABCD$ -
$\angle A=\angle D$ and $\angle B=\angle C$

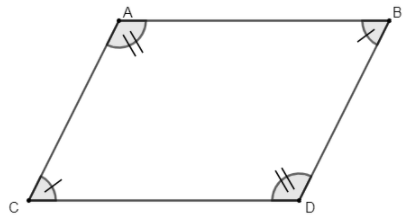
(ii) In any parallelogram, sum of adjacent angles is $180{}^\circ $, like in $ABCD$ -
$\angle A+\angle B=180{}^\circ $
$\angle B+\angle D=180{}^\circ $
$\angle C+\angle D=180{}^\circ $
$\angle A+\angle C=180{}^\circ $
Now, let us get started with the solution.
According to the figure given, we have $PQRS$, $TMUS$ and $VNWS$ are parallelograms, and \[\angle PQR=52{}^\circ \]

As we know that, opposite angles in any parallelogram are equal, so in $PQRS$-
\[\angle PQR=\angle PSR\]
\[\therefore \angle PSR=52{}^\circ \]
Similarly, in $TMUS$ we can write that
\[\angle TMU=\angle TSU\]
From this, we know that we can write \[\angle TSU=\angle PSR=52{}^\circ \]
\[\therefore \angle TMU=52{}^\circ \]
And in $VNWS$,
\[\angle VNW=\angle VSW\]
\[\because \angle VSW=\angle PSR=52{}^\circ \]
\[\Rightarrow \angle VNW=52{}^\circ \]
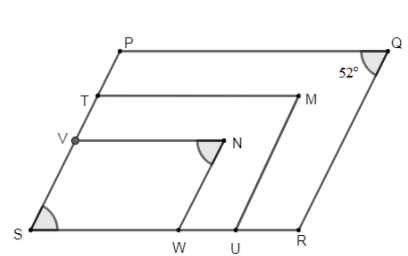
Now, the figure is as below –

We know that the adjacent angles in a parallelogram are supplementary to each other. This means the sum of adjacent angles in a parallelogram is $180{}^\circ $.
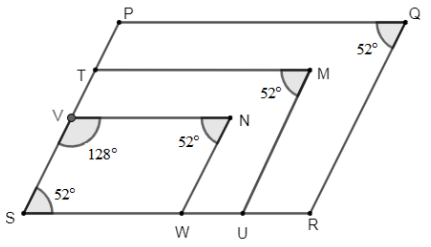
So, in $VNWS$, we can write that
\[\angle SVN+\angle VNW=180{}^\circ \]
As, we have \[\angle VNW=52{}^\circ \], we can write that
\[\angle SVN+52{}^\circ =180{}^\circ \]
$\Rightarrow \angle SVN=180{}^\circ -52{}^\circ $
$\Rightarrow \angle SVN=128{}^\circ $
So, the difference between $\angle TMU$ and $\angle SVN$ $=\angle SVN-\angle TMU$
As, $\angle SVN=128{}^\circ $ and \[\angle TMU=52{}^\circ \]
$\Rightarrow \angle SVN-\angle TMU$
$=128{}^\circ -52{}^\circ $
$=76{}^\circ $
So, the difference between $\angle TMU$ and $\angle SVN$ is$76{}^\circ $. Hence, the correct option is (c).

Note: Students should take care that which angles are adjacent and which are opposite to each other. In this type of question, properties are very important. So, keep in mind which properties are for adjacent angles, and which properties are for opposite angles. And at last, don’t forget to check calculation mistakes, otherwise,1 the entire question will be wrong.