Question

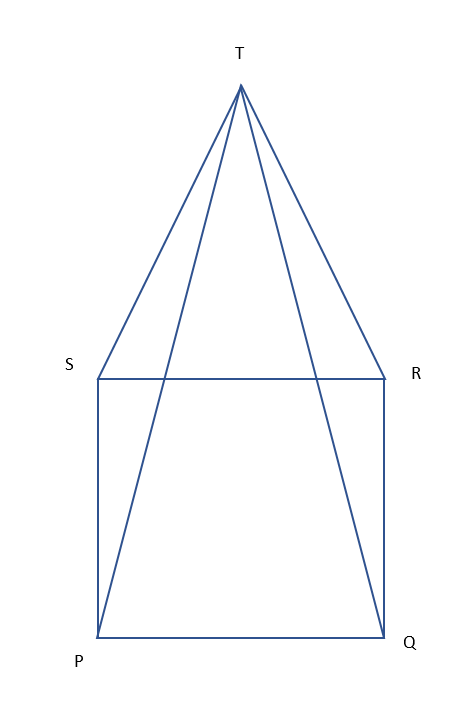
In the given figure, PQRS is a square and SRT is an equilateral triangle. Prove that $\angle TQR = {15^ \circ }$

Answer 1

Hint: We will first make use of the fact that the sides of an equilateral triangle are equal and then use the fact that sides of a square are equal as well. Now, we will sum all the angles using angle sum property and do some modifications to get the required answer.

Step-By-Step answer:
Since, SRT is an equilateral triangle.
Therefore, SR = RT = ST ……………(1)
Since SR is the side of a square. So, SR = RQ = QP = PS ………….(2)
Using the equations (1) and (2), we will then obtain:-
$ \Rightarrow $ SR = RT = ST = RQ = QP = PS
In $\vartriangle TRQ$:-
Since TR = RQ
$ \Rightarrow \angle TQR = \angle QTR$ [Because angles opposite to equal sides in a triangle are equal] ………..(3)
In $\vartriangle TRQ$:-
$ \Rightarrow \angle QTR + \angle TQR + \angle TRQ = {180^ \circ }$ (By Angle Sum Property)
We can rewrite this as:-
$ \Rightarrow \angle QTR + \angle TQR + \angle TRS + \angle SRQ = {180^ \circ }$
Since the angle SRQ is an angle of a square, therefore, it is a right angle.
$ \Rightarrow \angle QTR + \angle TQR + \angle TRS + {90^ \circ } = {180^ \circ }$
Taking the 90 from addition in left hand side to subtraction in right hand side, we will then obtain the following expression:-
$ \Rightarrow \angle QTR + \angle TQR + \angle TRS = {180^ \circ } - {90^ \circ }$
Simplifying the calculations on the right hand side, we will then obtain:-
$ \Rightarrow \angle QTR + \angle TQR + \angle TRS = {90^ \circ }$
Now, we will use equation (3) in the above expression, we will then obtain:-
$ \Rightarrow \angle TQR + \angle TQR + \angle TRS = {90^ \circ }$
Summing up the like terms in the left hand side, we will then obtain:-
$ \Rightarrow 2\angle TQR + \angle TRS = {90^ \circ }$ ………………..(4)
Since $\angle TRS$ is an angle of an equilateral triangle, therefore it is ${60^ \circ }$ in measure.
$ \Rightarrow \angle TRS = {60^ \circ }$
Putting this in the equation (4), we will then obtain:-
$ \Rightarrow 2\angle TQR + {60^ \circ } = {90^ \circ }$
Taking the ${60^ \circ }$ from the addition in left hand side to subtraction in the right hand side, we will then obtain:-
$ \Rightarrow 2\angle TQR = {90^ \circ } - {60^ \circ }$
Clubbing the like terms in the right hand side, we will then obtain:-
$ \Rightarrow 2\angle TQR = {30^ \circ }$
$ \Rightarrow \angle TQR = \dfrac{{{{30}^ \circ }}}{2} = {15^ \circ }$

Hence, proved.

Note: The students must note that we know that in an equilateral triangle, all the sides and all the angles are equal.
Since all the angles are equal, let one angle be x. Then sum all of them and put the sum equal to ${180^ \circ }$, then we will get x to be equal to ${60^ \circ }$.
The students must remember that all the sides of an equilateral triangle and a square are always equal.