Question

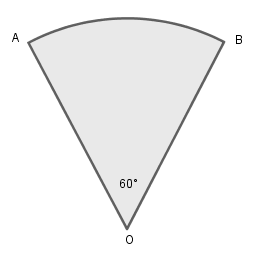
In the given figure of the sector of a circle of radius 10.5 cm, what is the perimeter of the sector?

Answer 1

Hint: To find the perimeter of any shape, we will find the length around that shape. Here a sector of the circle is given in the diagram. To find the perimeter of the sector, we need to find the length of the curved path which is known as Arc as the length of the straight line which is equal to radius is already given. Adding them will give the required answer.

Complete step by step solution:
In the given figure, $OABO$ is a sector of a circle of radius $r=10.5cm$ and $\angle AOB = {30^ \circ }$.
As we know that length of arc of a sector of a circle is $\dfrac{\theta }{{{{360}^ \circ }}}.2\pi r$, where $r$= radius of circle and $\theta$ is the angle made by arc at the centre of circle.
$AB = \dfrac{{{{60}^ \circ }}}{{{{360}^ \circ }}}2 \times 3.14 \times 10.5cm$ $ = 395.64cm$
Now the perimeter of sector $OABO$ will be equals to,
$ OA + {\text{Arc}}AB + OB $
On substituting the corresponding values we get,
$\Rightarrow (10.5 + 395.64 + 10.5)cm $
$416.64cm $

$\therefore$ The perimeter of the given sector is 416.64cm

Note:
A circular sector of circle sector (symbol: ⌔), is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector. In the diagram, θ is the central angle, r is the radius of the circle, and L is the arc length of the minor sector.
A sector with the central angle of 180° is called a half-disk and is bounded by a diameter and a semicircle. Sectors with other central angles are sometimes given special names, these include quadrants (90°), sextants (60°) and octants (45°), which come from the sector being one 4th, 6th or 8th part of a full circle, respectively. Confusingly, the arc of a quadrant can also be termed a quadrant.
1. The area bounded by two radii and an arc is called the sector of a circle.
2. The perimeter of sector is given by $\dfrac{\theta }{{{{360}^ \circ }}}.2\pi r$
3. The area of sector is given by $\dfrac{\theta }{{{{360}^ \circ }}}.\pi {r^2}$