Question

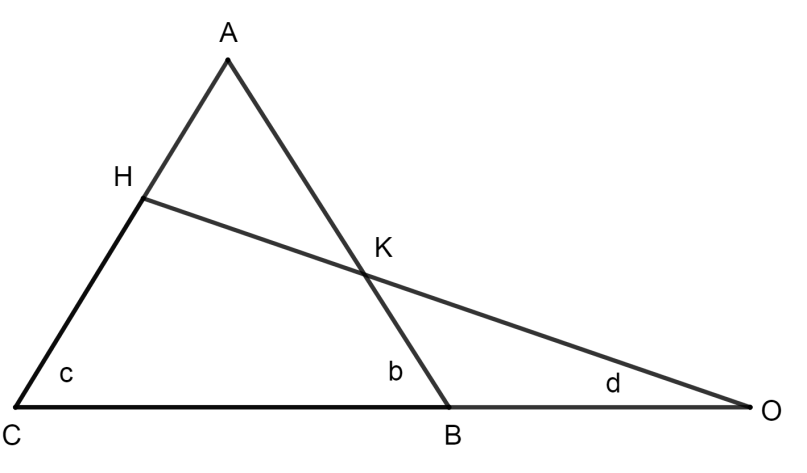
In the given figure, OBC and OKH are straight lines. If AH=AK, \[b={{80}^{\circ }}\]and \[c={{30}^{\circ }}\]the value of d is

$\begin{align}
  & (a){{20}^{\circ }} \\
 & (b){{25}^{\circ }} \\
 & (c){{30}^{\circ }} \\
 & (d){{45}^{\circ }} \\
\end{align}$

Answer 1

Hint: In the above question, we will find the third angle of a triangle using the fact that the sum of all interior angles of a triangle is \[{{180}^{\circ }}\]. Also, we will use the property that, if two sides of a triangle are equal then their angle opposite to the equal sides are also equal.

Complete step by step answer:
We have been given that a figure and in that, OBC and OKH are straight lines and AH=AK, \[b={{80}^{\circ }}\] and \[c={{30}^{\circ }}\] then we have to find the value of d.

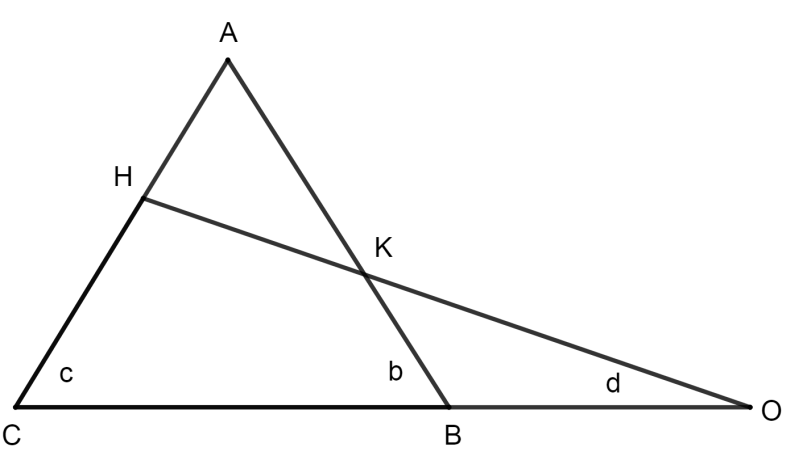
We know that the sum of interior angle of a triangle is equal to \[{{180}^{\circ }}\]. So, in \[\Delta ABC,\]we can apply this as shown below,
\[\begin{align}
  & \angle A+b+c={{180}^{\circ }} \\
 & \angle A+{{80}^{\circ }}+{{30}^{\circ }}={{180}^{\circ }} \\
 & \angle A+{{110}^{\circ }}={{180}^{\circ }} \\
 & \angle A={{180}^{\circ }}-{{110}^{\circ }} \\
 & \angle A={{70}^{\circ }} \\
\end{align}\]
Now, in\[\Delta AHK,AH=AK\]. So, using property that the angles opposite to equal sides are also equal, we can write that \[\angle AHK=\angle AKH.\]
So, by using the property that the sum of interior angle of a triangle is equal to \[{{180}^{\circ }}\], we can again write
\[\Rightarrow \angle A+\angle AHK+\angle AKH={{180}^{\circ }}\]
We know that $\angle AHK=\angle AKH.$ So, we can modify the above equation as
\[\begin{align}
  & {{70}^{\circ }}+2\angle AHK={{180}^{\circ }} \\
 & 2\angle AHK={{180}^{\circ }}-{{70}^{\circ }} \\
 & 2\angle AHK={{110}^{\circ }} \\
 & \angle AHK=\dfrac{{{110}^{\circ }}}{2} \\
 & \angle AHK={{55}^{\circ }} \\
\end{align}\]
So, we have got \[\angle AHK=\angle AKH={{55}^{\circ }}\]
Now, the line AHC is a straight line and so it forms a linear pair. Therefore, we get that
\[\begin{align}
  & \angle AHK+\angle OHC={{180}^{\circ }} \\
 & {{55}^{\circ }}+\angle OHC={{180}^{\circ }} \\
 & \angle OHC={{180}^{\circ }}-{{55}^{\circ }} \\
 & \angle OHC={{125}^{\circ }} \\
\end{align}\]
In \[\Delta OHC,\] we have \[\angle OHC={{125}^{\circ }},c={{30}^{\circ }}\text{ and }\angle \text{HOC=d}\text{.}\]
Using the internal sum property of a triangle, we get,
\[\begin{align}
  & {{125}^{\circ }}+{{30}^{\circ }}+d={{180}^{\circ }} \\
 & {{155}^{\circ }}+d={{180}^{\circ }} \\
 & d={{180}^{\circ }}-{{155}^{\circ }} \\
 & d={{25}^{\circ }} \\
\end{align}\]
Here, the value of d is \[{{25}^{\circ }}\].
Therefore, the correct option is B.

Note:
We can also solve the given question if we consider the \[\Delta OBK,\] and use the fact that \[\angle OKB=\angle AKH\] since these are vertically opposite angles. We have already calculated it as \[\angle AHK=\angle AKH={{55}^{\circ }}\] as per solution. Then we can find \[\angle KBO\] by using the fact that OBC is a straight line and angle B is a linear pair. So, since we have \[b={{80}^{\circ }}\] , we can find \[\angle KBO={{180}^{\circ }}-\angle KBC\Rightarrow {{180}^{\circ }}-{{80}^{\circ }}\Rightarrow {{100}^{\circ }}\] . Now, again considering \[\Delta OBK,\] we have two angles, so third angle, i.e d can be found using the fact that sum of interior angles of a triangle is equal to \[{{180}^{\circ }}\]. Therefore, we have
\[\begin{align}
  & \angle KBO+\angle KOB+\angle BOK={{180}^{\circ }} \\
 & \Rightarrow {{100}^{\circ }}+d+{{55}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow d={{180}^{\circ }}-{{100}^{\circ }}-{{55}^{\circ }} \\
 & \Rightarrow d={{25}^{\circ }} \\
\end{align}\]