Question

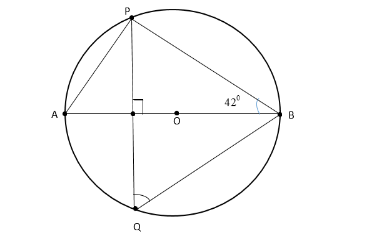
In the given figure, O is the centre of the circle. Find the value of \[\angle PQB\] .

Answer 1

Hint: In a triangle there are three angels. We know that the sum of all angels in the triangle is equal to 180 degrees. In the right angle triangle one of the angles is 90 degrees and the other two will have a sum of the degree equal to 90 degrees. We also have a theorem that angels of the same segment of a circle are equal.

Complete step-by-step answer:
Now from the diagram take \[\Delta APB\] . We have
 \[\angle APB = {90^0}\] because it is angle in a semicircle and \[\angle PBA = {42^0}\] .
 \[ \Rightarrow \angle PAB + \angle PBA + \angle APB = {180^0}\]
This is because, from the angle sum property of a triangle we have that the sum of three angels in a triangle is equal to 180 degree.
 \[ \Rightarrow \angle PAB + {42^0} + {90^0} = {180^0}\]
 \[ \Rightarrow \angle PAB = {180^0} - {42^0} - {90^0}\]
Using simple addition and subtraction we get,
 \[ \Rightarrow \angle PAB = {48^0}\]
If we see in the diagram \[\angle PAB\] and \[\angle PQB\] are the same segment of circle, then by the theorem we have that angels of the same segment of a circle are equal.
That is, \[\angle PAB = \angle PQB\]
Therefore \[\angle PQB = {48^0}\] .
So, the correct answer is “\[\angle PQB = {48^0}\]”.

Note: In solving these types of problems we have to know which theorem is suitable for the problem. Without the use of theorem it will be difficult to solve. Know the meaning of alternative angles and corresponding angles. Angels of the same segment of a circle are equal, we can prove this using the fact that angle subtended by an arc at the centre is double the angle subtended by it at any other point on the circle.