Question

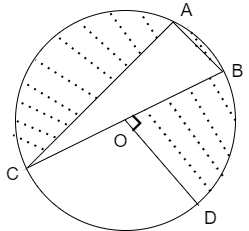
In the given figure, O is the centre of the circle with \[AC=24cm\], \[AB=7cm\] and \[\angle BOD={{90}^{\circ }}\] then find the area of shaded region.

Answer 1

Hint: We solve this problem by using the area formula of circle, triangle and quarter circle.
The area of triangle is given as
\[A=\dfrac{1}{2}\left( base \right)\left( height \right)\]
The area formula of circle having the radius \['r'\] is given as
\[A=\pi {{r}^{2}}\]
The area formula of quarter circle is given as
\[A=\dfrac{\pi {{r}^{2}}}{4}\]
We use the condition that is the angle formed by the diameter on the circle is \[{{90}^{\circ }}\] then we use the Pythagoras theorem to find the value of radius of the circle. The Pythagoras Theorem states that the square of hypotenuse is equal to sum of squares of other two sides that is for the triangle shown below

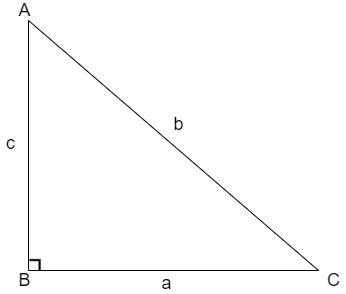
The Pythagoras theorem is given as\[{{b}^{2}}={{a}^{2}}+{{c}^{2}}\].

Complete step by step answer:
We are given the lengths that is \[AC=24cm\], \[AB=7cm\]
We know that the condition that the angle formed by the diameter on the circle is \[{{90}^{\circ }}\]
Here from the figure we can see that the line segment CB is diameter of the circle.
So, by using the above condition we can say that
\[\Rightarrow \angle CAB={{90}^{\circ }}\]
Now, let us consider the triangle \[\Delta ABC\]
We know that the Pythagoras Theorem states that the square of hypotenuse is equal to sum of squares of other two sides that is for the triangle shown below

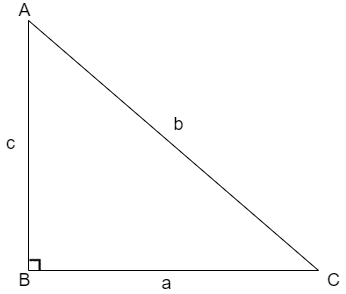
The Pythagoras theorem is given as\[{{b}^{2}}={{a}^{2}}+{{c}^{2}}\].
Now, by applying the Pythagoras theorem to \[\Delta ABC\] we get
\[\Rightarrow C{{B}^{2}}=C{{A}^{2}}+A{{B}^{2}}\]
Now, by substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow C{{B}^{2}}={{24}^{2}}+{{7}^{2}} \\
 & \Rightarrow C{{B}^{2}}=576+49 \\
 & \Rightarrow CB=\sqrt{625}=25 \\
\end{align}\]
Here we can see that the length of CB is 25cm which is the diameter of the circle.
We know that the radius of the circle is half the diameter.
Let us assume that the radius of the circle as \['r'\] then we get
\[\begin{align}
  & \Rightarrow r=\dfrac{BC}{2} \\
 & \Rightarrow r=\dfrac{25}{2}cm \\
\end{align}\]
Now, let us consider the triangle \[\Delta ABC\]
Let us assume that the area of the triangle \[\Delta ABC\] as \[{{A}_{1}}\]
We know that the area of triangle is given as
\[A=\dfrac{1}{2}\left( base \right)\left( height \right)\]
By using the above formula to triangle \[\Delta ABC\] we get
\[\Rightarrow {{A}_{1}}=\dfrac{1}{2}\left( AC \right)\left( AB \right)\]

Now, by substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow {{A}_{1}}=\dfrac{1}{2}\times 24\times 7 \\
 & \Rightarrow {{A}_{1}}=12\times 7 \\
 & \Rightarrow {{A}_{1}}=84c{{m}^{2}} \\
\end{align}\]
Now, let us consider the sector OCD
Let us assume that the area of sector OCD as \[{{A}_{2}}\]
Here we can see that the sector OCD is quarter circle because \[\angle BOD={{90}^{\circ }}\]
We know that the area formula of quarter circle is given as
\[A=\dfrac{\pi {{r}^{2}}}{4}\]
By using the above formula we get the area of OCD as
\[\Rightarrow {{A}_{2}}=\dfrac{\pi {{r}^{2}}}{4}\]
We know that the value of \[\pi \] is 3.14 and radius is \[\dfrac{25}{2}\]
By substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow {{A}_{2}}=\dfrac{3.14{{\left( \dfrac{25}{2} \right)}^{2}}}{4} \\
 & \Rightarrow {{A}_{2}}=\dfrac{3.14\times 625}{4\times 4} \\
 & \Rightarrow {{A}_{2}}=122.65c{{m}^{2}} \\
\end{align}\]
Now, let us assume that the area of the whole circle as \[A\]
We know that the area formula of circle having the radius \['r'\] is given as
\[A=\pi {{r}^{2}}\]
By using this formula we get the area of circle as
\[\Rightarrow A=\pi {{r}^{2}}\]
We know that the value of \[\pi \] is 3.14 and radius is \[\dfrac{25}{2}\]
By substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow A=3.14{{\left( \dfrac{25}{2} \right)}^{2}} \\
 & \Rightarrow A=3.14\times \dfrac{625}{4} \\
 & \Rightarrow A=490.625c{{m}^{2}} \\
\end{align}\]
Now, let us assume that the area of the shaded region as \[x\]
Here we can see that the area of circle is the combination of areas of triangle, quarter circle and shaded region.
By converting the above statement into mathematical equation we get
\[\Rightarrow A={{A}_{1}}+{{A}_{2}}+x\]
By substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow 490.625=84+122.65+x \\
 & \Rightarrow x=490.625-206.65 \\
 & \Rightarrow x=283.975c{{m}^{2}} \\
\end{align}\]

Therefore we can conclude that the area of the shaded region is \[283.975c{{m}^{2}}\]

Note: In this solution we used many formulas and the conditions for solving this problem.
We need to remember these general points because these are very commonly used conditions and formulas. The important conditions that we used in this problem are
(1) The angle formed by the diameter on the circle is \[{{90}^{\circ }}\]
(2) The area formula of quarter circle is given as
\[A=\dfrac{\pi {{r}^{2}}}{4}\]
(3) The Pythagoras Theorem states that the square of hypotenuse is equal to sum of squares of other two sides that is for the triangle shown below

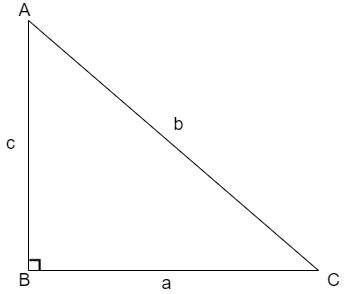
The Pythagoras theorem is given as\[{{b}^{2}}={{a}^{2}}+{{c}^{2}}\].
These conditions and formulas are very basic which are used very commonly.
We should not make mistakes in these basics.
Some students may make mistakes in application of these formulas to problems.