Question

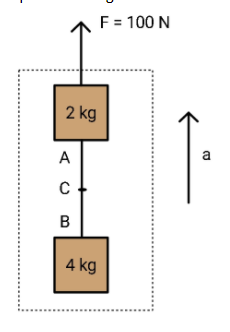
In the given figure mass of string AB is 2 kg. Find tensions at A, B and C, where C is the midpoint of string.

Answer 1

Hint: Consider drawing free body diagrams for different segments in question. Start by considering the entire system to be an isolated block and determine the acceleration for the entire system first.

Complete answer:
We first take the sum of all the masses involved i.e., 2 kg of the string, total 6 kg for the two blocks should give us, total mass of 8 kg. Now this mass happens to be moving by an acceleration determined by considering the free body equation:

$Ma = F - W$,
as weight W of the entire system acts downwards and F is pulling the system upwards. For simplification, we determine W to be 80 N for the system as we consider g to be 10 ms$^{-2}$. The acceleration for the entire system is:
$a = \dfrac{100 - 80}{8} = 2.5 ms^{-2}$
(we are already given F = 100 N).
This is the acceleration with which all the components inside the system are moving.
Now we break the problem into three segments and construct the following three cases.

1. To determine the tension at point A, consider the following free body diagram consisting of the entire chain length AB and the mass underneath it of 4 kg.

Looking at the diagram, we may write:
$T - W_A = m_A a$
where $m_A$ is the mass beneath point and $W_A$ is the weight for it.
The mass concerned here, happens to be 2 kg of the string and 4 kg of the block so,
$m_A = 6 kg$ and $W_A = 60 N$.
Keeping the values in the free body equation we had, we get:
$T = (6 \times 2.5)N + 60 N = 75 N$.
This means that tension at point A is 75 N.

2. Now, point C happens to be at the midpoint of the string, so we take only half the mass of the string i.e., 1 kg and we have the 4 kg block too, so,
$m_C = 5 kg$ and $W_C = 50 N$.
We have the free body diagram same as before, but the equation now becomes:
$T - W_C = m_C a$.
Keeping the values we get:
$T = (5 \times 2.5) N + 50 N = 62.5 N$.
This means that attention at point C is 62.5 N.

3. For point B, the free body diagram now consists of only the block of 4 kg.

The equation for this is:
$T - W_B = m_B a$
where $m_B = 4 kg$ and $W_B = 40 N$ has to be used, giving us:
$T = (4 \times 2.5) N + 40 N = 50 N$.
Therefore the tension in the string at point B is 50 N.

Note:
In writing the free body equation we considered the upward force direction to be positive and downward force direction to be negative. We write the resultant force as the sum of forces acting on the body.