Question

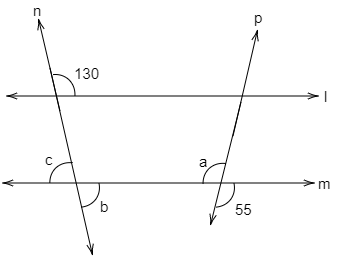
In the given figure, lines $l\parallel m$ and lines p and n are traverses. Find the measure of $\angle a,\angle b,\angle c$ using the measure of angle given figure.

Answer 1

Hint: Here we will have to apply concepts of the sum of all the angles on a straight line is $180^\circ$, Corresponding angles are the angles which are formed in matching corners or corresponding corners with the transversal when two parallel lines are intersected by any other line & vertically opposite angles are equal when two lines intersect. Applying this concept of geometry, we can get values of angles asked for in the above question.

Complete step by step answer:
Given: - l and m are parallel lines ($l\parallel m$) intersected by transversals n and p respectively.
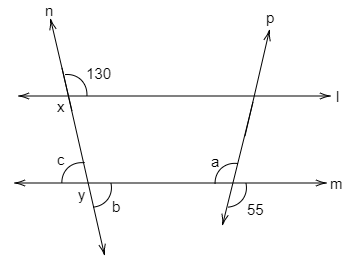
Let the intersection point of n with l and m be x and y.

Before solving this question, one must be familiar with some of the following explained terms:-
PARALLEL LINES: Two lines are said to be parallel if they do not meet, no matter how much they are extended in either direction.
TRANSVERSAL LINE: When a line cuts two or more parallel or non-parallel lines, that line is called a transversal line.
In this figure, $\angle nxl$ and $\angle xym$ are corresponding angles.
We know that corresponding angles are the angles that are formed in matching corners or corresponding corners with the transversal when two parallel lines are intersected by any other line.
$ \Rightarrow \angle xym = \angle nxl$
Substitute the values,
$ \Rightarrow \angle xym = 130^\circ $
We need to know that, Sum of all the angles on a straight line is $180^\circ $.
In the above figure, on line segment n,
$ \Rightarrow \angle xym + b = 180^\circ $
Substitute the value,
$ \Rightarrow 130^\circ + b = 180^\circ $
Move the constant part on the right side,
$ \Rightarrow b = 180^\circ - 130^\circ $
Subtract the value,
$\therefore b = 50^\circ $
In this figure, $b$ and $c$ are vertically opposite angles.
We know that vertically opposite angles are equal when two lines intersect.
$ \Rightarrow c = b$
Substitute the value,
$\therefore c = 50^\circ $
In this figure, $a$ and $55^\circ $ are vertically opposite angles.
We know that vertically opposite angles are equal when two lines intersect.
$\therefore a = 55^\circ $

Hence, the value is $a = 55^\circ ,b = 50^\circ ,c = 50^\circ $.

Note: When two parallel lines are cut by transversal lines:
1. Alternate exterior angles are equal.
2. Alternate interior angles are equal.
3. Corresponding angles are equal.
4. Co-interior angles are supplementary.
5. Exterior angles are supplementary.