Question

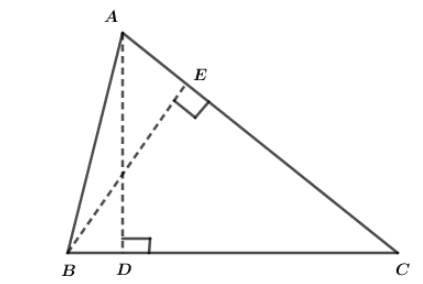
In the given figure, in ∆ABC, segment AD and segment BE are altitudes and AE≅BD. Prove that segment AD≅BE.

Answer 1

Hint: Here, we can use the properties of triangles. First prove that triangle ADB and triangle BEA are congruent triangles by RHS (Right angle-Hypotenuse-side) property as two right angles are given as also AE≅BD. Then by applying CPCT (Corresponding parts of congruent triangles) property we can show that AD≅BE.

Complete step-by-step answer:
In triangles ADB and triangle BEA, we have
∠ADB = ∠BEA [Each equal to 90°]
Since, given that AD and BE are altitudes.
AB = AB [Common side in both the triangles]
BD = AE [Given]
By RHS (Right angle-Hypotenuse-side) congruence criteria triangle ADB and triangle BEA are congruent triangles.
[RHS congruence criteria states that if in two right triangles, their hypotenuse are equal, and any of one sides are equal then the two triangles are congruent triangles]
 ∆ADB≅∆BEA
Now, in two congruent triangles, their corresponding sides and corresponding angles are equal.
Therefore, AD≅BE.

Note:
In these types of questions, always use properties and theorems of triangles. You must be aware of different properties by which two triangles can be proved as congruent triangles like SSS (Side-Side-Side), Side-Angle-Side) and RHS (Right angle-Hypotenuse-side). Also you should be very careful between words like similar triangles and congruent triangles, as sometimes these two words may create confusion. Never go for any algebraic calculations with observing the triangles and also do not go for any trigonometric calculations (if any standard angles are given in figure) as it can make the solution more complicated. By using properties of triangles, we simply get the relation between the sides and angles of two triangles. Using properties of triangles you not only make the solution simpler but also easiest to understand.