Question

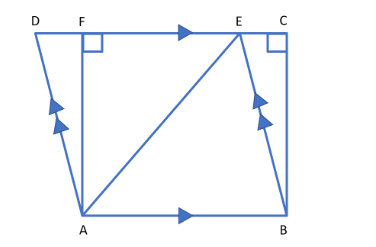
In the given figure, if the area of \[\Delta ADE\] is \[60{\text{ }}c{m^2};\] state, giving reason the area of rectangle ABCF.

A. \[120{\text{ }}c{m^2}\]
B. \[110{\text{ }}c{m^2}\]
C. \[100{\text{ }}c{m^2}\]
D. \[150{\text{ }}c{m^2}\]

Answer 1

Hint: To solve this question, we will start with using the value of the area of the triangle to get the value of its sides, then after getting that value, we will use it to find the value of the area of the rectangle. Here we will also use the important facts about parallelogram, hence with that we will get our required answer.

Complete step-by-step answer:
We have been given a figure, where the area of \[\Delta ADE\] is \[60{\text{ }}c{m^2};\] we need to find the area of the rectangle ABCF.
We know that, Area of triangle $ = \dfrac{1}{2} \times base \times height $
Here, we have, from the figure, base of the \[\Delta ADE\] \[ = \] DE
And, height of \[\Delta ADE\] \[ = \] AF
So, Area of \[\Rightarrow \Delta ADE = \dfrac{1}{2} \times DE \times AF = 60c{m^2}\]
\[DE \times AF = 120c{m^2}........eq.(1)\]
Since, we know that in the parallelogram, the diagonal bisects the parallelogram into two equal triangles.
Therefore, in parallelogram ABDE, AB \[ = \] DE
Now, we know that, Area of rectangle \[ = \] length \[ \times \] breadth
So, on putting the values in the above formula, we get
 $ \Rightarrow $ Area of rectangle ABCF \[ = {\text{ }}AB \times AF\]
\[ = {\text{ }}DE{\text{ }} \times {\text{ }}AF\] [Since, AB \[ = \] DE]
\[ = {\text{ }}120\;c{m^2}\] [by using \[eq.{\text{ }}\left( 1 \right)\]]
So, area of rectangle ABCF is \[120\;c{m^2}.\]
Thus, option (A) \[120{\text{ }}c{m^2}\] is correct.
So, the correct answer is “Option A”.

Note: Students should note that the first approach of solving these types of questions, where very less values are given, is to use whatever values we are given, and then using that particular value, to find more values, that way you will be able to get your required answer.
Parallelogram is a simple quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure.