Question

In the given figure if \[\angle ACE = {43^ \circ }\]and \[\angle CAF = {62^ \circ }\], find the value of a, b and c.

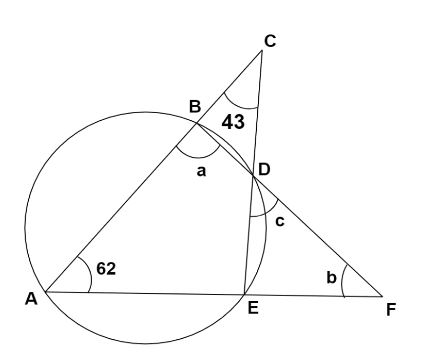
Answer 1

Hint: In the given figure, we need to find the values of a, b and c i.e. we need to find \[\angle ABF\], \[\angle BFA\] and \[\angle EDF\]. First of all, since we are given the measure of two angles in \[\vartriangle ACE\]. In order to find the measure of the third angle in \[\vartriangle ACE\], we will use angle sum property in \[\vartriangle ACE\]. Angle sum property states that Sum of angles in a triangle is equal to \[{180^ \circ }\]. By this, we will get \[\angle AEC\]. Now, since \[AF\] is a straight line, And \[\angle AEC\] and \[\angle CEF\] intersect at point \[E\]. So, they form a pair of linear angles. We know, the sum of linear angles is equal to \[{180^ \circ }\]. Using this property of linear pair of angles, we will find the measure of \[\angle CEF\]. After that, using the property of cyclic quadrilateral that sum of opposite angles in a cyclic quadrilateral is equal to \[{180^ \circ }\], we will have \[\angle ABD + \angle AEC = {180^ \circ }\] and so, we will find the measure of \[\angle ABD\]. Now, after this, we will have measure of two angles in \[\vartriangle ABF\] and so we can use angle sum property in \[\vartriangle ABF\], to find the measure of third angle i.e. \[\angle AFB\]. Also, in \[\vartriangle EDF\] we now have the measure of two angles with us and so to find the measure of the third angle, we will use angle sum property in \[\vartriangle EDF\] and we will get the desired answer.

Complete step by step answer:

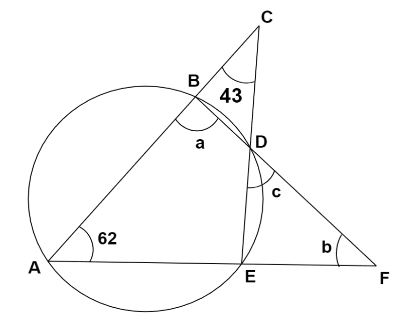
In \[\vartriangle ACE\], We are given \[\angle CAF = {62^ \circ }\]and \[\angle ACE = {43^ \circ }\]. Using Angle Sum Property in \[\vartriangle ACE\], we have
Sum of all angles in \[\vartriangle ACE\] is equal to \[{180^ \circ }\].
\[\angle ACE + \angle CAF + \angle AEC = {180^ \circ }\]
\[ \Rightarrow {43^ \circ } + {62^ \circ } + \angle AEC = {180^ \circ }\]

Now, solving left hand side we get
\[ \Rightarrow {105^ \circ } + \angle AEC = {180^ \circ }\]
Subtracting \[{105^ \circ }\] from both the sides, we get
\[ \Rightarrow {105^ \circ } + \angle AEC - {105^ \circ } = {180^ \circ } - {105^ \circ }\]
Clubbing the constant terms together on left hand side,
\[ \Rightarrow \angle AEC + ({105^ \circ } - {105^ \circ }) = {180^ \circ } - {105^ \circ }\]
\[ \Rightarrow \angle AEC + {0^ \circ } = {180^ \circ } - {105^ \circ }\]
As \[a + 0 = a\]. Using this and solving the right hand side, we get
\[ \Rightarrow \angle AEC = {75^ \circ } - - - - - - (1)\]
Now, \[\angle AEC\] and \[\angle FED\] intersect at a point \[E\] and \[AF\]is a straight line. Hence, \[\angle AEC\] and \[\angle FED\]form a pair of linear angles.

Using the property, Sum of angles forming linear pair is \[{180^ \circ }\], we have
\[\angle AEC + \angle FED = {180^ \circ }\]
Now, using (1) in above expression,
\[ \Rightarrow {75^ \circ } + \angle FED = {180^ \circ }\]
Subtracting \[{75^ \circ }\] from both the sides, we get
\[ \Rightarrow {75^ \circ } + \angle FED - {75^ \circ } = {180^ \circ } - {75^ \circ }\]
Clubbing the constant terms on left hand side and using the property \[a + 0 = a\],
\[ \Rightarrow \angle FED + ({75^ \circ } - {75^ \circ }) = {180^ \circ } - {75^ \circ }\]
\[ \Rightarrow \angle FED + {0^ \circ } = {105^ \circ }\]
\[ \Rightarrow \angle FED = {105^ \circ } - - - - - - (2)\]

We now see that \[ABDE\]is a cyclic quadrilateral. Using the property of cyclic quadrilateral that sum of opposite angles of a quadrilateral is equal to \[{180^ \circ }\], we have
\[\angle ABD + \angle AEC = {180^ \circ }\]
Now, using (1), we get
\[\angle ABD + {75^ \circ } = {180^ \circ }\]
Rearranging the terms, we get
\[ \Rightarrow \angle ABD = {180^ \circ } - {75^ \circ }\]
Now, solving Right Hand Side, we get
\[ \Rightarrow \angle ABD = {105^ \circ } - - - - - - (3)\]
Now, in \[\vartriangle ABF\], we have \[\angle CAF = \angle BAF = {62^ \circ }\] and \[\angle ABD = \angle ABF = {105^ \circ }\]
Using Angles Sum property in \[\vartriangle ABF\], we get
\[\angle ABF + \angle BAF + \angle BFA = {180^ \circ }\]

Substituting the values of the angles, we get
\[{105^ \circ } + {62^ \circ } + \angle AFB = {180^ \circ }\]
\[ \Rightarrow {167^ \circ } + \angle AFB = {180^ \circ }\]
Rearranging the terms, we get
\[ \Rightarrow \angle AFB = {180^ \circ } - {167^ \circ }\]
\[ \Rightarrow \angle AFB = {13^ \circ } - - - - - - (4)\]
Now, from (2) and (4), in \[\vartriangle EDF\], we have \[\angle FED = {105^ \circ }\] and \[\angle AFB = \angle EFD = {13^ \circ }\]
Using Angle Sum Property in \[\vartriangle EDF\], we get
\[\angle FED + \angle EFD + \angle EDF = {180^ \circ }\]

Substituting the values in above expression, we have
\[ \Rightarrow {105^ \circ } + {13^ \circ } + \angle EDF = {180^ \circ }\]
\[ \Rightarrow {118^ \circ } + \angle EDF = {180^ \circ }\]
Rearranging the terms, we get
\[ \Rightarrow \angle EDF = {180^ \circ } - {118^ \circ }\]
\[ \Rightarrow \angle EDF = {62^ \circ } - - - - - - (5)\]
Hence, from (3), (4) and (5), we have
\[\angle ABD = \angle ABF = {105^ \circ }\]
\[ \Rightarrow \angle AFB = {13^ \circ }\]
\[ \Rightarrow \angle EDF = {62^ \circ }\]

Putting these values in the above diagram,

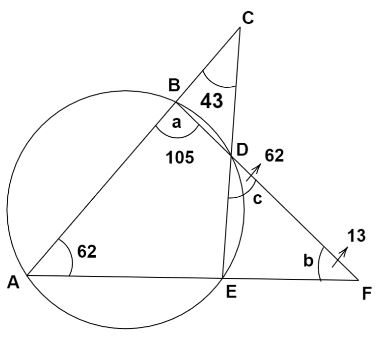
Therefore, we get \[a = {105^ \circ }\], \[b = {13^ \circ }\] and \[c = {62^ \circ }\].

Note: The sum of all the interior angles of a quadrilateral is equal to 360 degrees. The angle sum property of any n sided closed polygon is given by $\left( {n - 2} \right){180^ \circ }$. So, we can obtain the interior angle sum of a quadrilateral by substituting the value of n as two in the formula. The opposite angles of a cyclic quadrilateral are supplementary to each other as they add up to 180 degrees. Transposition method is useful in solving the equations for variables by shifting the terms from one side to another.