Question

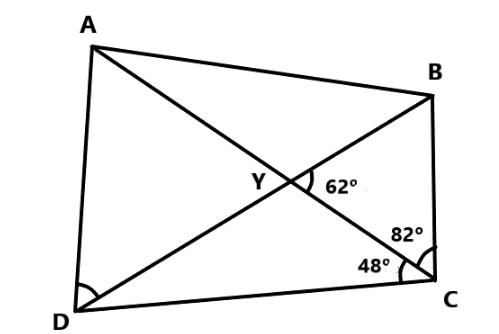
In the given figure, find the measure of $ \angle ABC $ , if ABCD is a cyclic quadrilateral.

a. $ {120^ \circ } $
b. $ {118^ \circ } $
c. $ {84^ \circ } $
d. $ {128^ \circ } $

Answer 1

Hint: Here in this question, we have to find the value of angle B. The ABCD is a cyclic quadrilateral, the cyclic quadrilateral means a quadrilateral inscribed into a circle whose vertices lie on a single circle. By using the properties of triangles, we find the value of the angle B.

Complete step-by-step answer:
In the question they have mentioned ABCD is a cyclic quadrilateral, the quadrilateral which is inscribed in the circle and whose vertices lie on the same circle. By figure we know the value of some angles by using this we have to determine the value of the angle B.
Now consider the $ \vartriangle BYC $ , we know the value of $ \angle Y $ and $ \angle C $ we can determine the value of $ \angle B $ . As we know that the sum of all angles in the triangle is $ {180^ \circ } $ . Therefore, we have $ \angle B + \angle Y + \angle C = {180^ \circ } $ .------- (1)
  $ \angle Y = {62^ \circ } $ and $ \angle C = {82^ \circ } $ are the known value. Substitute these values in the equation (1)
  $ \angle B + 62 + 82 = {180^ \circ } $
On applying the addition
 $ \Rightarrow \angle B + 144 = 180 $
Move 144 to the RHS
 $ \Rightarrow \angle B = 180 - 144 $
On further simplification
 $ \Rightarrow \angle B = 36 $
Therefore, in the triangle $ \vartriangle BYC $ the value of $ \angle B $ is $ {36^ \circ } $ .
We know the half value of angle B.
Also, $ \angle ACD = \angle ABD $ because the angles lie in the same segment.
Therefore the $ \Rightarrow \angle ABD = {48^ \circ } $
The angle $ \angle ABC = \angle ABD + \angle CBY $
Substituting the values, we get
 $ \Rightarrow \angle ABC = 48 + 36 $
On applying the addition, we get
 $ \Rightarrow \angle ABC = {84^ \circ } $
Therefore, the measure of $ \angle ABC $ , if ABCD is a cyclic quadrilateral is $ {84^ \circ } $
So, the correct answer is “Option C”.

Note: The ABCD is a quadrilateral, and it is cyclic quadrilateral since all the four sides inscribed in a circle lie on the circumference of a circle. Here we use some properties of triangles and the angles in the quadrilateral. By using these concepts, we can determine the solution for this question.