Question

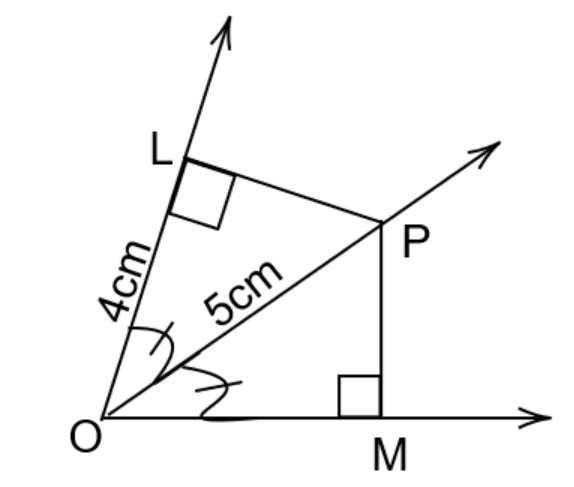
In the given figure , find \[PM\] .

\[\left( 1 \right)\] \[3cm\]
\[\left( 2 \right)\] \[5cm\]
\[\left( 3 \right)\] \[4cm\]
\[\left( 4 \right)\] \[2cm\]

Answer 1

Hint: We have to find the value of \[PM\] from the given figure using the given conditions . We will solve this question using the concept of congruent triangles and the concept of pythagoras theorem . First we will prove that the \[\Delta OLP\] and the \[\Delta OPM\] are congruent and then by proving the congruence between the two triangles we would compute that \[LP\] and \[PM\] are equal . And then using the pythagorean theorem we will find the value of \[LP\] and hence the value of \[PM\] .

Complete step-by-step solution:
Given :
\[\angle LOP = \angle MOP\]
Now , we will prove that the triangle LOP and triangle MOP are congruent .
In \[\Delta LOP\] and \[\Delta MOP\]
\[OP = OP\] [common side of the two triangles]
\[\angle LOP = \angle MOP\] [given]
\[\angle PLO = \angle PMO\] [both angles are equal to 90°]
\[\Delta LOP \cong \Delta MOP\]
[By Angle Side Angle (ASA) congruency]
Hence , proving that the both triangles are congruent .
So , from the properties of congruence of the triangles we can compute that
LP = MP [corresponding sides of congruent triangles are equal]
Now , using the pythagorean theorem , we know that the formula of pythagoras theorem is given as :
\[{\left( {base} \right)^2} + {\left( {perpendicular} \right)^2} = {\left( {hypotenuse} \right)^2}\]
Using the formula of pythagoras theorem , we get the value as :
\[{(OL)^2} + {(LP)^2} = {(OP)^2}\]
Putting the values in the formula , we get the value of \[LP\] as :
$(4)^2+(LP)^2=(5)^2$
\[\Rightarrow 16 + {(LP)^2} = 25\]
On further solving , we get the value of \[LP\] as :
\[{(LP)^2} = 25 - 16\]
\[\Rightarrow {(LP)^2} = 9\]
Taking square root , we get the value as :
\[LP = 3cm\]
As we proved that \[LP = PM\] , so the value of \[PM\] can be written as :
\[PM = 3cm\]
Hence , the value of \[PM\] is \[3cm\] .
Thus , the correct option is \[\left( 1 \right)\].

Note: Congruence of two triangles states that both the triangles are equal to each other i.e. both the corresponding sides of the triangle are equal , the corresponding angles of the triangles are also equal . We can prove the congruence of two triangles by different properties such as the SSS congruence ( Side Side Side congruence ) , AAA congruence ( Angle Angle Angle congruence ).