Question

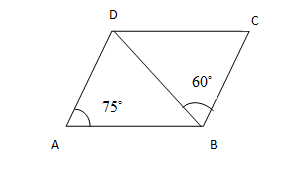
In the given figure, find $\angle BDC$ .

Answer 1

Hint: From the figure, the given quadrilateral is the parallelogram. In the parallelogram,
1. Opposite sides are parallel.
2. Opposite angles are equal.
$\therefore $ $\angle BAD = \angle BCD$ and,
$\angle CBA = \angle CDA$
Since we are given the angle $\angle BAD$ and $\angle BAD = \angle BCD$
$ \Rightarrow \angle BCD$is also known.
Apply the property of a triangle that is, Sum of all the angles of a triangle is ${180^ \circ }$.
$ \Rightarrow $ $\angle DBC + \angle BCD + \angle BDC = {180^ \circ }$
Since $\angle DBC$ is given and we have calculated$\angle BCD$, we can find $\angle BDC$ by substituting both the values into $\angle DBC + \angle BCD + \angle BDC = {180^ \circ }$.

Complete step by step answer:
According to the figure, let the quadrilateral ABCD is a parallelogram.
Consider the two angles are $\angle DBC = {60^ \circ }$ and $\angle BAD = {75^ \circ }$.
Since the given quadrilateral is a parallelogram, opposite sides of a parallelogram are parallel and opposite angles of a parallelogram are equal.
$\therefore $ $\angle BAD = \angle BCD$
Since $\angle BAD = {75^ \circ }$, $\therefore $ $\angle BCD = {75^ \circ }$.
Apply the property of a triangle that is, Sum of all the angles of a triangle is ${180^ \circ }$.
$ \Rightarrow $ $\angle DBC + \angle BCD + \angle BDC = {180^ \circ } \ldots (1)$
Substitute $\angle DBC = {60^ \circ }$ and $\angle BCD = {75^ \circ }$ into the equation $(1)$.
${60^ \circ } + {75^ \circ } + \angle BDC = {180^ \circ }$
$\angle BDC = {180^ \circ } - ({60^ \circ } + {75^ \circ })$
$\angle BDC = {180^ \circ } - {135^ \circ }$
$\angle BDC = {45^ \circ }$

The required angle is $\angle BDC = {45^ \circ }$.

Note: Students must remember that here we are using the important properties of the parallelogram that the opposite angles of a parallelogram are the same and opposite sides are parallel. From this, we can find one angle of the triangle BDC. Use the triangle property: The sum of all the angles of a triangle is ${180^ \circ }$.
In a triangle always look for the two angles and by using the triangle property we can find the unknown third angle.