
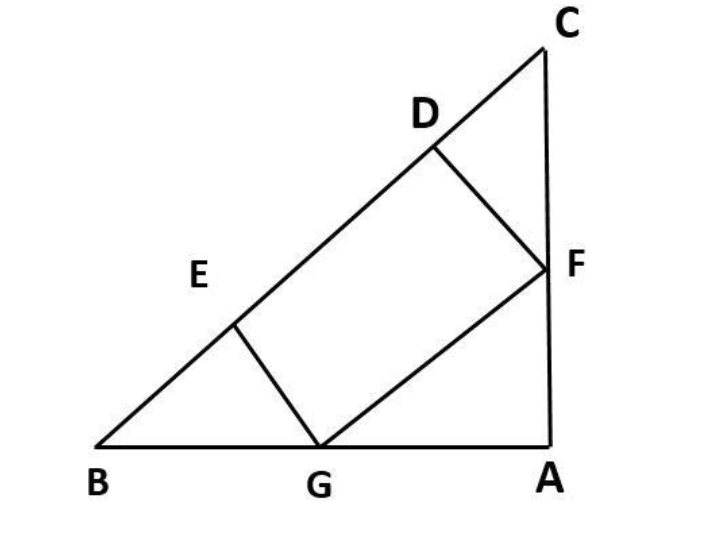
In the given figure, $DEFG$ is a square and $\angle BAC = 90^\circ $ show that $D{E^2} = BD \times EC$

Answer
576k+ views
Hint: To prove the given equation we use Angle-Angle test of similarity property i.e. AA test of similarity of triangles. Use the given information that DEFG is a square so its sides are equal and angles are ${90^0}$
Complete step-by-step answer:
According to the details given in the question we can draw a figure as follows,
In this question it is given that $\angle ABC = 90^\circ $ and we have to prove$D{E^2} = BD \times EC$
Now, proof
In $\Delta AFG$and $\Delta BDG$
$\Rightarrow \Rightarrow \angle AFG = \angle BDG$ . . . (since, both the angles are of $90^\circ $)
$\angle GAF = \angle DBG$ . . . [These are corresponding angles because $GF||BC$and $AB$is transversal. And we know that corresponding angles are equal]
Thus, by angle-angle $(AA)$ test of similarity of similarity of triangles, we can write
$\Delta AGF \approx \Delta EFG$ . . . . (i)
Now,
In $\Delta AFG$and $\Delta EFC$
$\Rightarrow \angle AFG = \angle CEF$ . . . (since, both the angles are $90^\circ $)
$\Rightarrow \angle AFG = \angle ECF$ . . . . (These are corresponding angles because $GF||BC$ and $AC$is transversal. And we know that the corresponding angles are equal)
And
Thus, by angle-angle $(AA)$ test of similarity of similarity of triangles, we can write
$\Delta AGF \approx \Delta EFC$ . . . . (ii)
From, equation (i) and (ii) we get,
$\Delta DBG \approx \Delta EFC$
$\Rightarrow \dfrac{{BD}}{{EF}} = \dfrac{{DG}}{{EC}}$.
And
$\dfrac{{BD}}{{DE}} = \dfrac{{DE}}{{EC}}$ . . . [$DEFG$is a square]
Therefore, on cross multiplying, we get an equation as,
$D{E^2} = EC \times BD$
Note: While checking for similarity, you have to make sure that you are checking for corresponding angle and corresponding sides. The word “corresponding” is very important in similarity. You cannot relate any other sides in case of similarity. So make sure you write the names of triangles in a proper way as well.
Complete step-by-step answer:
According to the details given in the question we can draw a figure as follows,

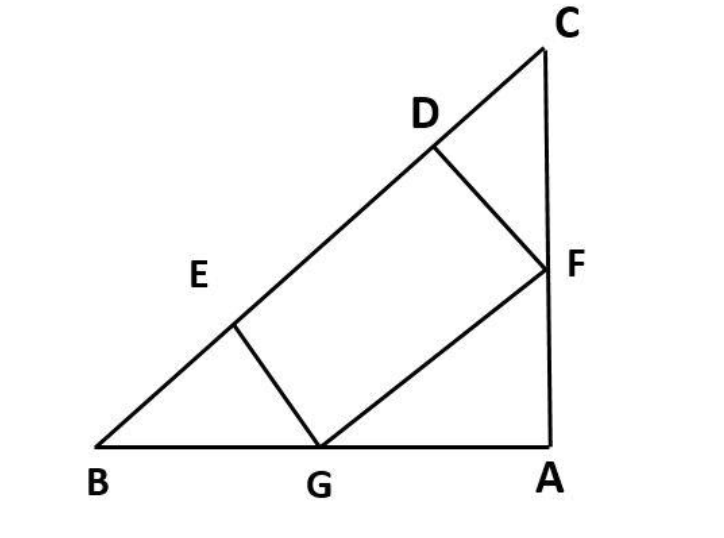
In this question it is given that $\angle ABC = 90^\circ $ and we have to prove$D{E^2} = BD \times EC$
Now, proof
In $\Delta AFG$and $\Delta BDG$
$\Rightarrow \Rightarrow \angle AFG = \angle BDG$ . . . (since, both the angles are of $90^\circ $)
$\angle GAF = \angle DBG$ . . . [These are corresponding angles because $GF||BC$and $AB$is transversal. And we know that corresponding angles are equal]
Thus, by angle-angle $(AA)$ test of similarity of similarity of triangles, we can write
$\Delta AGF \approx \Delta EFG$ . . . . (i)
Now,
In $\Delta AFG$and $\Delta EFC$
$\Rightarrow \angle AFG = \angle CEF$ . . . (since, both the angles are $90^\circ $)
$\Rightarrow \angle AFG = \angle ECF$ . . . . (These are corresponding angles because $GF||BC$ and $AC$is transversal. And we know that the corresponding angles are equal)
And
Thus, by angle-angle $(AA)$ test of similarity of similarity of triangles, we can write
$\Delta AGF \approx \Delta EFC$ . . . . (ii)
From, equation (i) and (ii) we get,
$\Delta DBG \approx \Delta EFC$
$\Rightarrow \dfrac{{BD}}{{EF}} = \dfrac{{DG}}{{EC}}$.
And
$\dfrac{{BD}}{{DE}} = \dfrac{{DE}}{{EC}}$ . . . [$DEFG$is a square]
Therefore, on cross multiplying, we get an equation as,
$D{E^2} = EC \times BD$
Note: While checking for similarity, you have to make sure that you are checking for corresponding angle and corresponding sides. The word “corresponding” is very important in similarity. You cannot relate any other sides in case of similarity. So make sure you write the names of triangles in a proper way as well.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




