Question

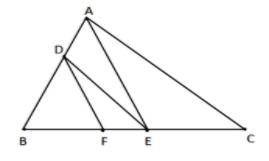
In the given figure $DE||AC$, $DF||AE$. If the lengths of BF and FE in cms are 4 and 5 respectively, then find the length of EC.

Answer 1

Hint:
To find the length of EC, take $\vartriangle BAE$ and in this triangle $DF||AE$. Apply basic proportionality theorem in it and find the ratio of BD and DA. After that take $\vartriangle ABC$ and in this triangle $DE||AC$. Applying basic proportionality theorem in this, we get the ratio of BE and EC. By equating both the equations we can find the length of EC.

Basic proportionality theorem (BPT):
It is also known as Thales theorem. According to BPT, if a line intersects two sides into two distinct points and is parallel to the third side then the line divides both the sides in proportional. E.g. in $\vartriangle ABC$ as given below $DE||BC$.

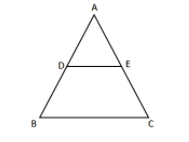
According to BPT, sides AD, DB, AE and EC are proportional i.e.
\[ \Rightarrow \dfrac{{AD}}{{DB}} = \dfrac{{AE}}{{EC}}\]

Complete step by step solution:
In this triangle we are given with a $\vartriangle ABC$ and in $\vartriangle ABC$$DE||AC$ and $DF||AE$.
Also, the length of BF and FE is given to us. i.e.
$ \Rightarrow BF = 4cm$ ……..(1)
$ \Rightarrow FE = 5cm$ ……….(2)
We have to find the length of side BC. The figure is given below:

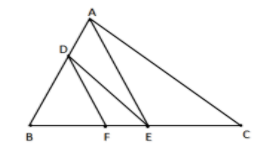
You can see above figure, in $\vartriangle BAE$ the sides $DF||AE$ and hence we can apply BPT on it and we get,
$ \Rightarrow \dfrac{{BD}}{{DA}} = \dfrac{{BF}}{{FE}}$
Now, put the value of BF and FE from (1) and (2), we get the ratio of BD and DA,
$ \Rightarrow \dfrac{{BD}}{{DA}} = \dfrac{4}{5}$ …………..(3)
You can see the figure, in $\vartriangle ABC$ the sides $DE||AC$ and hence we can apply BPT on it and we get,
$ \Rightarrow \dfrac{{BE}}{{EC}} = \dfrac{{BD}}{{DA}}$

Now, put the value of ratio of BD and DA (3), we get the ratio of BE and AC,
$ \Rightarrow \dfrac{{BE}}{{EC}} = \dfrac{4}{5}$
We can write BE as sum of BF and FE i.e.
$ \Rightarrow \dfrac{{BF + FE}}{{EC}} = \dfrac{4}{5}$
Put the value of BF and FE from (1) and (2), we get,
 $ \Rightarrow \dfrac{{4 + 5}}{{EC}} = \dfrac{4}{5}$
By adding the numbers in numerator, we get,
$ \Rightarrow \dfrac{9}{{EC}} = \dfrac{4}{5}$
By cross multiplication we will find the length of EC i.e.
$ \Rightarrow EC = \dfrac{{9 \times 5}}{4}$
By multiplying the numbers in numerator, we get,
$ \Rightarrow EC = \dfrac{{45}}{4}$
Divide numerator with denominator, we get,
$ \Rightarrow EC = 11.25cm$

Hence the length of EC is 11.25cm.

Note:
While applying BPT theorem it is noted that the ratio of sides should be taken in order otherwise your answer may get wrong i.e. if they take the ratio as $\dfrac{{DA}}{{BD}} = \dfrac{{BF}}{{FE}}$ then their answer will get wrong. So, take care of these types of mistakes.
Second, can you say that side BD is 4? No, as we can’t be sure about this. It may or may not be 4 as we have only found the ratio of BE and EC. But if they have given the value of EC then we can find BD also and vice-versa.