Question

In the given figure, chord AB is the diameter of the circle. What is the measure of the $\angle BDC$ ?

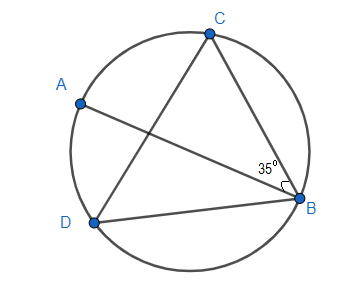
Answer 1

Hint: For solving the question, you need to use the property that the angles subtended by the same segment of the circle are equal, and the angle subtended by a diameter of the circle at the circumference is equal to $90{}^\circ $.

Complete step-by-step solution -
Let’s start by drawing a diagram with all the required constructions for our better visualisation.

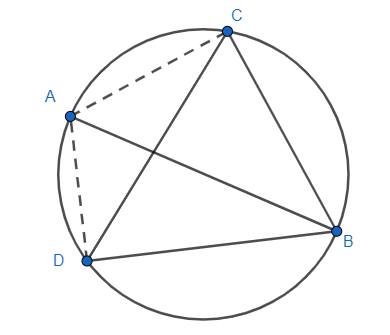
Now we know that the angles subtended by the same segment of the circle are equal and $\angle ABC\text{ and }\angle \text{ADC}$ are angles subtended by the same segment AC.
$\therefore \angle ABC=\angle ADC$
It is given in the question that $\angle ABC=15{}^\circ $ . If we combine this with above result, we get
 $\angle ABC=\angle ADC=15{}^\circ $
Now from the figure, we can see that $\angle ADB$ can be written as the sum of $\angle ADC\text{ and }\angle BDC$ . We also found that $\angle ADC=15{}^\circ $ . So, we can say:
$\angle BDC+\angle ADC=\angle ADB$
$\Rightarrow \angle BDC+15{}^\circ =\angle ADB$
Now, as it is given that AB is the diameter of the circle and we know angle subtended by a diameter of the circle at the circumference is equal to $90{}^\circ $ . So, we can say that $\angle ADB=90{}^\circ $ .
$\therefore \angle BDC+15{}^\circ =90{}^\circ $
$\Rightarrow \angle BDC=75{}^\circ $
Therefore, the measure of the $\angle BDC$ is equal to $75{}^\circ $ .

Note: It is prescribed to learn all the basic theorems related to circles as they are regularly used in the questions related to circles and cyclic quadrilaterals, as we did in the above question.